实验一
1.顺序表的初始化、查找、插入、删除、输出、撤销等操作
#include <stdio.h>
#include <stdlib.h>
#define ERROR 0
#define OK 1
#define Overflow 2
#define Underflow 3
#define NotPresent 4
#define Duplicate 5
typedef int ElemType;
typedef struct seqlist
{
int n; //元素个数
int maxlength; //最大允许长度
ElemType *element; //指针变量
} SeqList;
typedef int Status; //自定义类型
//初始化
/*
为顺序表L动态分配一维数组
若动态分配一维数组失败则返回ERROR(0)
*/
Status Init(SeqList *L,int mSize)
{
L->n=0;
L->maxlength=mSize;
L->element=(ElemType*)malloc(sizeof(ElemType)*mSize);
if(!L->element)
{
return ERROR;
}
return OK;
}
//顺序表的查找(查找元素ai的值,直接定位下标)
/*
首先判断传入的下标i是否越界(0~n-1)
若未越界,则取出element[i]的值传给x返回
算法复杂度为O(1)
*/
Status Find(SeqList L,int i,ElemType *x){
if(i<0||i>L.n-1){
return ERROR; //判断元素下标i是否越界
}
*x=L.element[i]; //取出element[i]的值通过参数x返回
return OK;
}
//顺序表的插入(在ai之后插入,即ai+1的位置)
/*
判断下标i是否越界 (-1~n-1)
判断顺序表存储空间是否已满
将元素ai+1~an-1依次向后移动一个位置
将要插入元素赋值给element[i+1]
表长+1
算法复杂度为O(n)
*/
Status Insert (SeqList *L, int i,ElemType x)
{
int j;
if(i<-1||i>L->n-1) //注意此处i的范围 是<-1 不是0 !!!
{
return ERROR;
}
if(L->n==L->maxlength) //判满
{
return ERROR;
}
for(j=L->n-1;j>i;j--) //通过循环将下标i+1到n-1的元素后移(从后往前)
{
L->element[j+1]=L->element[j]; //注意是j的值给j+1(从后往前)
}
L->element[i+1]=x; //把插入的 元素放到下标为 i+1 的位置
L->n=L->n+1; //表长加1
return OK;
}
//顺序表的删除
/*
判断下标是否越界(0~n-1)
判断顺序表是否为空
将元素ai+1~an-1依次前移一个位置
表长-1
算法复杂度为O(n)
*/
Status Delete(SeqList *L,int i)
{
int j;
if(i<0||i>L->n-1) return ERROR; //此处i<0!!!注意和插入区分
if(!L->n) return ERROR; //判空
for(j=i+1;j<L->n;j++)
{
L->element[j-1]=L->element[j]; //从前往后逐个前移元素,j的值给j-1
}
L->n--; //表长-1
return OK;
}
//顺序表的输出
Status Output(SeqList *L)
{
int i;
if(!L->n) return ERROR; //判空
for(i=0;i<L->n;i++)
{
printf("%d ",L->element[i]);
}
printf("\n\n");
return OK;
}
//顺序表的销毁
void Destroy(SeqList *L)
{
L->n=0;
L->maxlength=0;
free(L->element);
printf("Sucessfuly Destroyed!\n");
}
int main()
{
int i,j,k,x;
int m, n;
SeqList List;
k=Init(&List,100); //因为Init函数的形参是指针变量(地址),所以这里要用取地址符!!!
printf("初始化状态:%d\n\n",k); //测试返回值为 1
for(i=0;i<10;i++)
{
Insert(&List,i-1,i); //执行插入操作
}
Output(&List); // 0123456789
printf("请输入需要插入的数的位置下标和值(中间以空格隔开):\n");
scanf("%d%d",&m,&n);
Insert(&List,m,n);
printf("\n插入后的序列:\n");
Output(&List);
printf("请输入需要查找的数的下标:\n");
scanf("%d",&j);
Find(List,j,&x);
printf("\nThe value is : %d\n\n",x);
printf("请输入需要删除的数的下标:\n");
scanf("%d",&k);
Delete(&List,k);
printf("\n删除后的序列:\n");
Output(&List);
Destroy(&List);
printf("\n");
system("pause");
}
2.带表头结点单链表的初始化、查找、插入、删除、输出、撤销、逆置、排序等操作
#include<stdio.h>
#include<stdlib.h>
typedef int ElemType;
typedef int Status;
#define ERROR 0
#define OK 1
typedef struct Node { //结点的结构体
ElemType element; //结点的数据域
struct Node * link; //结点的指针域
}Node;
typedef struct headerlist{ //带表头结点的单链表结构体
struct Node* head; //表头结点
int n; //元素个数
}HeaderList;
//带表头结点单链表的初始化
Status Init(HeaderList *h) {
h->head=(Node*)malloc(sizeof(Node)); //生成表头结点
if(!h->head){
return ERROR;
}
h->head->link = NULL; //设置单链表为空表
h->n = 0;
return OK;
}
//带表头结点单链表的查找
/*
判断下标i是否越界 0~n-1
若未越界,则从头结点开始顺着单链表逐个结点查找
通过循环让p指向结点ai
将ai的值通过x返回
*/
Status Find(HeaderList *h,int i,ElemType *x){
Node *p;
int j;
if(i<0||i>h->n-1){
return ERROR;
}
p=h->head->link;
for(j=0;j<i;j++){
p=p->link;
}
*x=p->element;
return OK;
}
//带表头结点单链表的插入
/*
判断i是否越界 (-1~n-1)
查找ai,指针p指向此节点
生成一个新的结点q,将新结点的数据域置为x,指针q指向此结点
将q所指向的结点插入p所指的结点之后(注意不要断链)
单链表元素个数+1
*/
Status Insert(HeaderList *h, int i, ElemType x) {
Node *p, *q;
int j;
if (i<-1 || i>h->n - 1)
return ERROR;
p = h->head; //从头结点开始找ai元素所在的结点p
for (j = 0; j <= i; j++) {
p = p->link;
}
q = (Node*)malloc(sizeof(Node)); //生成新结点q
q->element = x;
q->link = p->link; //新结点q插在p之后
p->link = q;
h->n++;
return OK;
}
//带表头结点单链表的删除
/*
判断i是否越界(0~n-1)、单链表是否为空
查找元素ai的直接前驱ai-1,并令指针q指向它
则使p指向ai所在的结点,并删除ai
释放p所指结点的存储空间
单链表元素个数-1
*/
Status Delete(HeaderList *h,int i){
int j;
Node *p,*q;
if(!h->n){
return ERROR;
if(i<0||i>h->n-1){
return ERROR;
}
}
q=h->head;
for(j=0;j<i;j++){
q=q->link;
}
p=q->link; //p指向ai
q->link=p->link; //从单链表中删除p所指结点
free(p); //释放p所指结点的存储空间
h->n--;
return OK;
}
//带表头结点的输出操作
Status Output (HeaderList *h)
{
Node*p;
p = h->head;
for(int i=0; i<h->n; i++)
{
p = p->link;
printf("%d ",p->element);
}
printf("\n\n");
return OK;
}
// //带表头结点单链表的撤销操作
// void Destroy(HeaderList *h){
// Node *p,*q;
// while(h->head->link){
// q=h->head->link;
// p=h->head->link->link;
// free(h->head->link);
// h->head=q;
// }
// printf("Sucessfully destroyed!\n");
// }
void Destroy (HeaderList *h)
{
Node* p;
while(h->n)
{
p = h->head->link->link;
free(h->head->link);
h->head->link = p;
h->n -=1;
}
free(h->head);
printf("Sucessfully Destroyed!\n");
}
//将带表头结点单链表逆置
void Reverse(HeaderList *h){
Node *p,*q;
p = h->head->link; //p指向a0
h->head->link = NULL; //断开与表头结点的链接
while(p){
q=p->link; //q指向p的下一个结点
p->link=h->head->link;
h->head->link=p; //这两步主要是将p指向的结点插到头结点后面
p=q; //把下一个结点的地址给p(q的存在避免了断链)
}
}
//将单链表排序成为有序单链表
void Sort(HeaderList *h) //冒泡排序
{
int temp;
Node*p; //定义p.q两个结点,p指向第一个结点,q指向p的下一个结点
Node*q;
for(p=h->head->link;p!=NULL;p=p->link)
{
for(q=p->link,temp=0;q!=NULL;q=q->link)
{
if(p->element > q->element)
{
temp = p->element;
p->element = q->element; //如果p所指的结点的值大于q所指结点的值,则进行交换
q->element = temp;
}
}
}
}
//用于测试的主函数
int main()
{
int i;
int x;
int m,n,j,k;
HeaderList List;
i=Init(&List);
printf("初始化状态:%d\n\n",i); // 1
for(i=0;i<10;i++)
{
Insert(&List,i-1,i);
}
Output(&List); //0 1 2 3 4 5 6 7 8 9
printf("请输入需要插入的数的位置下标和值(中间以空格隔开):\n");
scanf("%d%d",&m,&n);
Insert(&List,m,n);
printf("\n插入后的序列:\n");
Output(&List);
Reverse(&List);
printf("逆置后的序列:\n");
Output(&List);
printf("排序后的序列:\n");
Sort(&List);
Output(&List);
printf("请输入需要查找的数的下标:\n");
scanf("%d",&j);
Find(&List,j,&x);
printf("The value is : %d\n\n",x);
printf("请输入需要删除的数的下标:\n");
scanf("%d",&k);
Delete(&List,k);
printf("删除后的序列:\n");
Output(&List);
Destroy(&List);
return 0;
}
3.一元多项式的创建、输出、撤销以及两个一元多项式相加和相乘
#include<stdio.h>
#include <stdlib.h>
typedef struct PNode
{
int coef;
int exp;
struct PNode *link;
} PNode;
typedef struct Polynominal
{
PNode *head;
} Polynominal;
void Create(Polynominal *p)
{
PNode *pn, *pre, *q;
p->head = (PNode*)malloc(sizeof(PNode));
p->head->exp = -1;
p->head->link = p->head;
for (;;)
{
pn = (PNode*)malloc(sizeof(PNode));
printf("coef\texp:\n");
scanf("%d\t%d",&pn->coef,&pn->exp);
if(pn->exp<0) //指数为负数时退出
break;
pre = p->head;
q = p->head->link;
while(q&&q->exp>pn->exp)
{
pre = q;
q = q->link;
}
pn->link = q;
pre->link = pn;
}
}
void Add(Polynominal *px,Polynominal *qx)
{
PNode *q, *q1 = qx->head, *p, *p1, *temp;
p = px->head->link;
q = q1->link;
while(p->exp<q->exp) //当p->exp<q->exp,则q所指的项成为结果多项式中的一项,q1和q分别右移一项
{
q1 = q;
q = q->link;
}
if(q->exp==p->exp) //当p->exp==q->exp,将系数coef相加,但需要讨论相加后系数是否为零
{
q->coef = p->coef + q->coef;
if(q->coef==0) //相加后系数为0
{
q1->link = q->link; //删除q
free(q); //释放q的空间
q = q1->link; //重置q指针
p = p->link; //p指针右移
}
else //相加后系数不为0
{
q1 = q;
q = q->link;
p = p->link;
}
}
else //当p->exp<q->exp,则复制p所指向的结点,并将其插在q1之后,指针p右移一项
{
temp = (PNode*)malloc(sizeof(PNode));//以p的系数和指数生成新的结点
temp->coef = p->coef;
temp->exp = p->exp;
temp->link = q1->link;
q1->link = temp;
q1 = q1->link;
p = p->link;
}
}
//多项式的乘法
void Multiply(Polynominal *px,Polynominal *qx){
Polynominal qx1,qx2;
PNode *q1,*q2,*q3,*q4,*pre,*q;
qx1.head = (PNode*)malloc(sizeof(PNode)); //生成新多项式qx1
qx1.head->exp = -1;
qx1.head->link = qx1.head; //qx1改造成循环链表
q1 = px->head->link; //q1指向px的第一项
q2 = qx->head->link; //q2指向qx的第一项
while(q2->exp != -1){ //当q2的指数不为-1时,px先和qx的每一项相乘
q3 = (PNode*)malloc(sizeof(PNode)); //q3存放相乘的结果
q3->coef = q1->coef * q2->coef;
q3->exp = q1->exp + q2->exp;
if(qx1.head->link->exp == -1){ //q3插入到qx1多项式第一项中
q3->link = qx1.head->link;
qx1.head->link = q3;
pre = qx1.head->link;
}
else{ //q3插入到qx1多项式最后一项中
q3->link = qx1.head;
pre->link = q3;
pre = pre->link;
}
q2 = q2->link;
}
q1 = q1->link; //q1后移一位
while(q1->exp != -1){ //将px剩下来每一项和qx每一项相乘
q2 = q2->link;
qx2.head = (PNode*)malloc(sizeof(PNode)); //生成新多项式qx2
qx2.head->exp = -1;
qx2.head->link = qx2.head;
while(q2->exp != -1){
q4 = (PNode*)malloc(sizeof(PNode));
q4->coef = q1->coef * q2->coef;
q4->exp = q1->exp + q2->exp;
if(qx2.head->link->exp == -1){
q4->link = qx2.head->link;
qx2.head->link = q4;
pre = qx2.head->link;
}
else{
q4->link = qx2.head;
pre->link = q4;
pre = pre->link;
}
q2 = q2->link;
}
Add(&qx2,&qx1); //利用加法合并同类项
q1 = q1->link;
}
Output(qx1);
}
void Output(Polynominal p){
PNode *q;
int flag = 1; //记录是否为第一项
q = p.head->link;
if (!q){
return;
}
while(q != p.head){
if (!flag && (q->coef > 0)) printf("+"); //在非第一项的正系数前输出+号
flag = 0; //flag置为0,表示不是第一项
if(q->coef == 0){ //当前项系数为0
return;
}
printf("%d",q->coef); //当前项系数不为0
switch(q->exp){ //判断当前项指数
case 0:break; //当前项指数为0,退出
case 1:printf("X");break; //当前项指数为1,输出X
default:printf("X^%d",q->exp);break; //当前项指数不为0,也不为1
}
q = q->link;
}
}
int main()
{
Polynominal *p,*q;
int x;
printf("Please enter the first polynomial:\n");
Create(&p);
Output(p);
printf("\n\nPlease enter the second polynomial:\n");
Create(&q);
Output(q);
printf("\n\nPlease choose the function:(0:ADD;1:MULTIPLY)\n");
scanf("%d",&x);
switch(x){
case 0:printf("Add Result:\n");
Add(&p,&q);
Output(q);
break;
case 1:printf("Multiply Result:\n");
Multiply(&p,&q);
Output(q);
default:break;
}
return 0;
}
实验二
1.二叉树的基本操作
a) 已知二叉树二叉链表结点结构定义如下:
typedef struct btnode
{
ElemType element;
struct btnode *lChild;
struct btnode *rChild;
} BTNode;
参照程序5.1~5.4,编写程序,完成二叉树的先序创建、先序遍历、中序遍历、后序遍历等操作。
b)基于上一实验内容中构建的二叉链表存储结构,编写程序实现求二叉树结点个数、叶结点个数、二叉树的高度以及交换二叉树所有子树的操作。
源码:
#include<stdio.h>
#include <stdlib.h>
typedef struct PNode
{
int coef;
int exp;
struct PNode *link;
} PNode;
typedef struct Polynominal
{
PNode *head;
} Polynominal;
void Create(Polynominal *p)
{
PNode *pn, *pre, *q;
p->head = (PNode*)malloc(sizeof(PNode));
p->head->exp = -1;
p->head->link = p->head;
for (;;)
{
pn = (PNode*)malloc(sizeof(PNode));
printf("coef\texp:\n");
scanf("%d\t%d",&pn->coef,&pn->exp);
if(pn->exp<0) //指数为负数时退出
break;
pre = p->head;
q = p->head->link;
while(q&&q->exp>pn->exp)
{
pre = q;
q = q->link;
}
pn->link = q;
pre->link = pn;
}
}
void Add(Polynominal *px,Polynominal *qx)
{
PNode *q, *q1 = qx->head, *p, *p1, *temp;
p = px->head->link;
q = q1->link;
while(p->exp<q->exp) //当p->exp<q->exp,则q所指的项成为结果多项式中的一项,q1和q分别右移一项
{
q1 = q;
q = q->link;
}
if(q->exp==p->exp) //当p->exp==q->exp,将系数coef相加,但需要讨论相加后系数是否为零
{
q->coef = p->coef + q->coef;
if(q->coef==0) //相加后系数为0
{
q1->link = q->link; //删除q
free(q); //释放q的空间
q = q1->link; //重置q指针
p = p->link; //p指针右移
}
else //相加后系数不为0
{
q1 = q;
q = q->link;
p = p->link;
}
}
else //当p->exp<q->exp,则复制p所指向的结点,并将其插在q1之后,指针p右移一项
{
temp = (PNode*)malloc(sizeof(PNode));//以p的系数和指数生成新的结点
temp->coef = p->coef;
temp->exp = p->exp;
temp->link = q1->link;
q1->link = temp;
q1 = q1->link;
p = p->link;
}
}
//多项式的乘法
void Multiply(Polynominal *px,Polynominal *qx){
Polynominal qx1,qx2;
PNode *q1,*q2,*q3,*q4,*pre,*q;
qx1.head = (PNode*)malloc(sizeof(PNode)); //生成新多项式qx1
qx1.head->exp = -1;
qx1.head->link = qx1.head; //qx1改造成循环链表
q1 = px->head->link; //q1指向px的第一项
q2 = qx->head->link; //q2指向qx的第一项
while(q2->exp != -1){ //当q2的指数不为-1时,px先和qx的每一项相乘
q3 = (PNode*)malloc(sizeof(PNode)); //q3存放相乘的结果
q3->coef = q1->coef * q2->coef;
q3->exp = q1->exp + q2->exp;
if(qx1.head->link->exp == -1){ //q3插入到qx1多项式第一项中
q3->link = qx1.head->link;
qx1.head->link = q3;
pre = qx1.head->link;
}
else{ //q3插入到qx1多项式最后一项中
q3->link = qx1.head;
pre->link = q3;
pre = pre->link;
}
q2 = q2->link;
}
q1 = q1->link; //q1后移一位
while(q1->exp != -1){ //将px剩下来每一项和qx每一项相乘
q2 = q2->link;
qx2.head = (PNode*)malloc(sizeof(PNode)); //生成新多项式qx2
qx2.head->exp = -1;
qx2.head->link = qx2.head;
while(q2->exp != -1){
q4 = (PNode*)malloc(sizeof(PNode));
q4->coef = q1->coef * q2->coef;
q4->exp = q1->exp + q2->exp;
if(qx2.head->link->exp == -1){
q4->link = qx2.head->link;
qx2.head->link = q4;
pre = qx2.head->link;
}
else{
q4->link = qx2.head;
pre->link = q4;
pre = pre->link;
}
q2 = q2->link;
}
Add(&qx2,&qx1); //利用加法合并同类项
q1 = q1->link;
}
Output(qx1);
}
void Output(Polynominal p){
PNode *q;
int flag = 1; //记录是否为第一项
q = p.head->link;
if (!q){
return;
}
while(q != p.head){
if (!flag && (q->coef > 0)) printf("+"); //在非第一项的正系数前输出+号
flag = 0; //flag置为0,表示不是第一项
if(q->coef == 0){ //当前项系数为0
return;
}
printf("%d",q->coef); //当前项系数不为0
switch(q->exp){ //判断当前项指数
case 0:break; //当前项指数为0,退出
case 1:printf("X");break; //当前项指数为1,输出X
default:printf("X^%d",q->exp);break; //当前项指数不为0,也不为1
}
q = q->link;
}
}
int main()
{
Polynominal *p,*q;
int x;
printf("Please enter the first polynomial:\n");
Create(&p);
Output(p);
printf("\n\nPlease enter the second polynomial:\n");
Create(&q);
Output(q);
printf("\n\nPlease choose the function:(0:ADD;1:MULTIPLY)\n");
scanf("%d",&x);
switch(x){
case 0:printf("Add Result:\n");
Add(&p,&q);
Output(q);
break;
case 1:printf("Multiply Result:\n");
Multiply(&p,&q);
Output(q);
default:break;
}
return 0;
}
2.哈夫曼编码/译码系统的实现
已知哈夫曼树结点结构定义如下:
typedef struct hfmTNode //哈夫曼树结点结构体
{
ElemeTypeBefore element; //结点的数据域
int w; //结点的权值
struct hfmTNode* lChild; //结点的左孩子指针
struct hfmTNode* rChild; //结点的右孩子指针
}HFMTnode;
编写程序,实现哈夫曼树的创建、哈夫曼编码及解码的实现。
源码:
#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
#include<string.h>
typedef char ElemeTypeBefore;
typedef struct hfmTNode //哈夫曼树结点结构体
{
ElemeTypeBefore element; //结点的数据域
int w; //结点的权值
struct hfmTNode* lChild; //结点的左孩子指针
struct hfmTNode* rChild; //结点的右孩子指针
}HFMTnode;
typedef struct hfmTree //哈夫曼树结构体
{
hfmTNode* root;
}HFMTree;
typedef HFMTree ElemeType;
typedef struct priorityQueue //优先权队列结构体
{
ElemeType *element;
int n;
int maxSize;
}PriorityQueue;
char res[50];
//创建一个优先权队列
void CreatPQ(PriorityQueue* PQ, int mSize)
{
PQ->maxSize = mSize;
PQ->n = 0;
PQ->element = (ElemeType*)malloc(mSize*sizeof(ElemeType));
}
//销毁一个优先权队列
void Destroy(PriorityQueue* PQ)
{
free(PQ->element);
PQ->n = 0;
PQ->maxSize = 0;
}
//判空
bool IsEmpty(PriorityQueue* PQ)
{
if(PQ->n == 0) return true;
return false;
}
//判满
bool IsFull(PriorityQueue* PQ)
{
if(PQ->n == PQ->maxSize) return true;
return false;
}
//向上调整
void AdjustUp(ElemeType heap[], int current)
{
int p = current;
ElemeType temp;
while(p>0)
{
if(heap[p].root->w<heap[(p-1)/2].root->w)
{
temp = heap[p];
heap[p] = heap[(p-1)/2];
heap[(p-1)/2] = temp;
p = (p-1)/2;
}
else break;
}
}
//在优先权队列中添加一个新元素x
void Append(PriorityQueue* PQ, ElemeType x)
{
if(IsFull(PQ)) return;
PQ->element[PQ->n] = x;
PQ->n++;
AdjustUp(PQ->element,(PQ->n)-1);
}
//向下调整
void AdjustDown(ElemeType heap[],int current,int n)
{
int i = current;
ElemeType temp;
while(2*i+1<n)
{
if(heap[i].root->w>heap[2*i+1].root->w)
{
temp = heap[i];
heap[i] = heap[2*i+1];
heap[2*i+1] = temp;
i = 2*i+1;
}
else break;
}
}
//取出堆顶哈夫曼结点并赋值给x
void Serve(PriorityQueue* PQ, ElemeType* x)
{
if(IsEmpty(PQ)) return;
*x = PQ->element[0];
PQ->n--;
PQ->element[0] = PQ->element[PQ->n];
AdjustDown(PQ->element, 0, PQ->n);
}
//新建一个哈夫曼结点
HFMTnode* NewNode(ElemeTypeBefore x, HFMTree* ln, HFMTree* rn, int w)
{
HFMTnode* p =(HFMTnode*)malloc(sizeof(HFMTnode));
p->element = x;
if(ln)p->lChild = ln->root;else p->lChild = NULL;
if(rn)p->rChild = rn->root;else p->rChild = NULL;
p->w = w;
return p;
}
//建树
void MakeHFMTree(HFMTree *bt, ElemeTypeBefore e, HFMTree *left, HFMTree *right, int w)
{
bt->root = NewNode(e, left, right, w);
if(bt->root || left == right)
return;
left->root = right->root = NULL; //root属于指针,置NULL可以减少内存使用
}
//创建哈夫曼树
HFMTree CreatHFMTree(int w[],char c[],int m)
{
PriorityQueue PQ; //定义优先权队列PQ,用于存放二叉树根结点指针
HFMTree x,y,z; //x,y,z为哈夫曼树变量
CreatPQ(&PQ,m); //初始化优先权队列PQ
for(int i=0; i<m; i++)
{
MakeHFMTree(&x,c[i],NULL,NULL,w[i]); //创建仅包含根结点的二叉树,w[i]为权值,c[i]为字符
Append(&PQ,x); //将新创建的二叉树插入优先权队列
}
while (PQ.n>1)
{
Serve(&PQ,&x); //从PQ中取出根结点值最小和次小的二叉树,分别存入x和y
Serve(&PQ,&y);
if(x.root->w>y.root->w) //设置左子树根结点的权值小于右子树
MakeHFMTree(&z,'#',&y,&x,x.root->w+y.root->w);
else
MakeHFMTree(&z,'#',&x,&y,x.root->w+y.root->w);
Append(&PQ,z); //将和并生成的新二叉树z插入优先权队列
}
Serve(&PQ,&x); //获取优先权队列中唯一的一棵二叉树,存入x,该二叉树即为哈夫曼树
return x;
}
//先序遍历
void PreOrderTree(HFMTnode *t){
if(t==NULL){
return;
}
printf("%c%d\t",t->element,t->w); //打印输出根结点,此处可以定义其他操作
PreOrderTree(t->lChild); //然后先序遍历左子树
PreOrderTree(t->rChild); //最后先序遍历右子树
}
//中序遍历
void InOrderTree(HFMTnode *t){
if(t==NULL){
return;
}
InOrderTree(t->lChild); //中序遍历根结点的左子树
printf("%c%d\t",t->element,t->w); //打印输出根结点,此处可以定义其他操作
InOrderTree(t->rChild); //最后中序遍历根结点的右子树
}
//哈夫曼编码
void Encode(HFMTnode *root,int level)
{
if(root->rChild==root->lChild)
{
if(level==0) //根结点
{
res[0]='0';
level++;
}
res[level]='\0'; //结束字符串
printf("%c => %s\n",root->element,res);
}
else
{
res[level]='0';
Encode(root->lChild,level+1);
res[level]='1';
Encode(root->rChild,level+1);
}
}
//解码
void Decode(HFMTnode *root, char a[])
{
int i,j;
HFMTnode *temp; //用来存放根结点,因为后续要重新从根结点进行匹配
temp = root;
int Len = strlen(a); //获取码文长度
for (i = 0; i < Len;i++)
{
if(a[i]=='0') //扫描到0则向根结点的左子树前进
{
if(root->lChild!=NULL)
{
root = root->lChild;
}
}else if (a[i]=='1') //扫描到1则向根结点的有子树前进
{
if(root->rChild!=NULL)
{
root = root->rChild;
}
}
if(root->lChild==NULL&&root->rChild==NULL) //当匹配到的是叶子结点
{
printf("%c",root->element); //输出对应字符
root = temp; //回到根结点
}
}
printf("\n");
}
int main()
{
HFMTree x;
int m,i;
int w[50]; //权值集
char c[50]; //字符集
char res[50];
char array[50];
printf("Please enter the number of characters:\n");
scanf("%d",&m);
for (i = 0; i < m;i++)
{
printf("Please enter %dth characters and weights (separated by commas):\n",i+1);
scanf(" %c,%d",&c[i],&w[i]);
}
x = CreatHFMTree(w,c,m);
printf("\n PreOrderHFMTree:\n");
PreOrderTree(x.root); //通过先序遍历和中序遍历的结果就可以画出这棵哈夫曼树
printf("\n InOrderHFMTree:\n");
InOrderTree(x.root);
printf("\n\nAfter Huffman coding:\n");
Encode(x.root,0);
printf("\nPlease enter the code text:\n");
scanf("%s",array);
printf("\nDecoding is:\n");
Decode(x.root,array);
return 0;
}
实验三
1.图的邻接矩阵存储及深度优先和宽度优先遍历
a) 已知图的邻接矩阵结构定义如下:
//邻接矩阵的结构体定义
typedef struct mGraph{
ElemType **a; //邻接矩阵
int n; //图的当前顶点数
int e; //图的当前边数
ElemType noEdge; //两顶点间无边时的值
}mGraph;
参照程序9.1~9.4,编写程序,完成邻接矩阵的初始化、撤销和边的搜索、插入、删除等操作。
b)以上述邻接矩阵为存储结构,编写程序,实现图的深度、宽度优先遍历。
源码:
#include<stdio.h>
#include<stdlib.h>
#include<math.h>
#include<windows.h>
#include<queue>
#define ERROR 0
#define OK 1
#define Overflow 2 //表示上溢
#define Underflow 3 //表示下溢
#define NotPresent 4 //表示元素不存在
#define Duplicate 5 //表示有重复元素
typedef int ElemType;
typedef int Status;
//邻接矩阵的结构体定义
typedef struct mGraph{
ElemType **a; //邻接矩阵
int n; //图的当前顶点数
int e; //图的当前边数
ElemType noEdge; //两顶点间无边时的值
}mGraph;
//循环队列的结构体定义
typedef struct{
int front;
int rear;
int maxSize; //最大容量
ElemType *element;
}Queue;
//创建一个能容纳mSize个单元的空队列
void Create(Queue *Q,int mSize){
Q->maxSize=mSize;
Q->element=(ElemType*)malloc(sizeof(ElemType)*mSize);
Q->front=Q->rear=0;
}
//判断队列是否为空,若是,则返回TRUE;否则返回FALSE
BOOL IsEmpty(Queue *Q){
return Q->front==Q->rear;
}
//判断队列是否已满,若是,则返回TRUE,否则返回FALSE
BOOL IsFULL(Queue *Q){
return (Q->rear+1)%Q->maxSize==Q->front;
}
//获取队头元素,并通过x返回.若操作成功,则返回TRUE,否则返回FALSE
BOOL Front(Queue *Q,ElemType *x){
if(IsEmpty(Q)) //空队列处理
return FALSE;
*x=Q->element[(Q->front+1)%Q->maxSize];
return TRUE;
}
//入队.在队列Q的队尾插入元素x(入队操作)。操作成功,则返回TRUE,否则返回FALSE
BOOL EnQueue(Queue *Q,ElemType x){
if(IsFULL(Q)) //溢出处理
return FALSE;
Q->rear=(Q->rear+1)%Q->maxSize;
Q->element[Q->rear]=x;
return TRUE;
}
//出队.从队列Q中删除队头元素(出队操作)。操作成功,则返回TRUE,否则返回FALSE
BOOL DeQueue(Queue *Q){
if(IsEmpty(Q)){ //空队列处理
return FALSE;
}
Q->front=(Q->front+1)%Q->maxSize;
return TRUE;
}
//邻接矩阵的初始化
Status Init(mGraph *mg,int nSize,ElemType noEdgeValue){
int i,j;
mg->n = nSize; //初始化顶点数
mg->e = 0; //初始化时没有边
mg->noEdge = noEdgeValue; //初始化没有边时的取值
mg->a = (ElemType**)malloc(nSize*sizeof(ElemType *)); //生成长度为n的一维指针数组
if(!mg->a) return ERROR;
for(i = 0;i < mg->n;i ++){ //动态生成二维数组
mg->a[i] = (ElemType*)malloc(nSize*sizeof(ElemType));
for(j = 0;j < mg->n;j ++){
mg->a[i][j] = mg->noEdge;
}
mg->a[i][i] = 0; //自回路设置为0
}
return OK;
}
//邻接矩阵的撤销,先释放一维数组,再释放指针数组
int Destory(mGraph *mg){
int i;
for(i = 0;i < mg->n;i ++){
free(mg->a[i]); //释放n个一维数组的存储空间
}
free(mg->a); //释放一维数组的存储空间
return 1;
}
//邻接矩阵的边的搜索
Status Exist(mGraph *mg,int u,int v){
if(u < 0||v < 0||u > mg->n-1||v > mg->n-1 ||u == v||mg->a[u][v] == mg->noEdge) return ERROR;
return OK;
}
//邻接矩阵的边的插入
Status Insert(mGraph *mg,int u,int v,ElemType w){
if(u < 0||v < 0||u > mg->n-1||v > mg->n-1 ||u == v) return ERROR;
if(mg->a[u][v] != mg->noEdge) return Duplicate; //若待插入边已存在,则返回出错信息
mg->a[u][v] = w; //插入新边
mg->e ++; //增加一条边
return OK;
}
//邻接矩阵的边的删除
Status Remove(mGraph *mg,int u,int v){
if(u < 0||v < 0||u > mg->n-1||v > mg->n-1 ||u == v) return ERROR;
if(mg->a[u][v] == mg->noEdge) return NotPresent; //若待删除边不存在,则返回出错信息
mg->a[u][v] = mg->noEdge; //删除边
mg->e --;
return OK;
}
//邻接矩阵的单一顶点DFS
void DFS(int v,int visited[],mGraph g){
int j;
printf("%d ",v); //访问顶点v
visited[v] = 1; //为顶点v打上访问标记
for(j = 0;j < g.n; j++){ //遍历v的邻接点
if(!visited[j] && g.a[v][j] > 0){ //当未被访问且有权值
DFS(j,visited,g);
}
}
}
//邻接矩阵的全图DFS
void DFSGraph(mGraph g){
int i;
int *visited = (int*)malloc(g.n * sizeof(int)); //动态生成标记数组visted
for(i = 0;i < g.n;i ++){
visited[i] = 0; //visted数组初始化
} //visted数组初始化
for(i = 0;i < g.n;i ++){ //逐一检查每个顶点,若未被访问,则调用DFS
if(!visited[i]){ //当未被访问且有权值
DFS(i,visited,g);
}
}
free(visited); //释放visted数组
}
//邻接矩阵的单一顶点BFS
void BFS(int v,int visited[],mGraph g){
Queue q;
Create(&q,g.n); //初始化队列
visited[v] = 1; //为顶点v打上访问标记
printf("%d ",v); //访问顶点v
EnQueue(&q,v); //将顶点v放入队列
while(!IsEmpty(&q)){
Front(&q,&v);
DeQueue(&q); //队首顶点出队列
for(int i = 0;i < g.n;i ++){ //遍历v的每一项
if(!visited[i] && g.a[v][i] > 0){ //若未被访问且有权值,则将其访问并放入队列,注意这里判断的是g.a[v][i]二维数组
visited[i] = 1;
printf("%d ",i);
EnQueue(&q,i);
}
}
}
}
//邻接矩阵的全图BFS
void BFSGraph(mGraph g){
int i;
int *visited = (int*)malloc(g.n * sizeof(int)); //动态生成visited数组
for(i = 0;i < g.n;i ++){ //初始化visited数组
visited[i] = 0;
}
for(i = 0 ;i < g.n;i ++){ //逐一检查每个顶点,若未被访问,则调用BFS
if(!visited[i]){
BFS(i,visited,g);
}
}
free(visited);
}
void OutPut(mGraph g)
{
int i, j;
printf(" ");
for (j = 0; j < g.n; j++)
printf("%4d", j);
printf("\n");
for (i = 0; i < g.n; i++)
{
printf("%d", i);
for (j = 0; j < g.n; j++)
printf("%4d", g.a[i][j]);
printf("\n");
}
}
int main(){
mGraph g;
int nSize,edge,u,v,i;
ElemType w;
printf("Please enter the size of the mgraph:");
scanf("%d",&nSize);
Init(&g,nSize,-1);
printf("Please enter the number of the edges:");
scanf("%d",&edge);
printf("Now init the graph.\n");
for(i = 0;i < edge;i ++){
printf("Please enter the %dth edge:",i);
scanf("%d%d%d",&u,&v,&w);
Insert(&g,u,v,w);
}
// nSize = 6;
// edge = 10;
// Init(&g,nSize,-1);
// Insert(&g,0,1,50);
// Insert(&g,0,2,10);
// Insert(&g,0,4,80);
// Insert(&g,1,2,15);
// Insert(&g,1,4,20);
// Insert(&g,2,3,15);
// Insert(&g,3,1,20);
// Insert(&g,3,4,45);
// Insert(&g,5,3,9);
// Insert(&g,5,4,10);
printf("\n\nThe adjacency matrix is:\n\n");
OutPut(g);
printf("\n");
printf("DFS:\n");
DFSGraph(g);
printf("\nBFS:\n");
BFSGraph(g);
// system("pause");
return 0;
}
2.图的邻接表存储及深度优先和宽度优先遍历
a)已知图的邻接表结构定义如下:
//邻接表的结构体定义
typedef struct ENode{
int adjVex; //任意顶点u相邻的顶点
ElemType w; //边的权值
struct ENode *nextArc; //指向下一个边结点
}ENode;
typedef struct{
int n; //图的当前顶点数
int e; //图的当前边数
ENode **a; //指向一维指针数组
}LGraph;
参照程序9.6~9.10,编写程序,完成邻接表的初始化、撤销和边的搜索、插入、删除等操作。
b)以上述邻接表为存储结构,编写程序,完成图的深度、宽度优先遍历。
源码:
#include<stdio.h>
#include<stdlib.h>
#include <windows.h>
#define ERROR 0
#define OK 1
#define Overflow 2 //表示上溢
#define Underflow 3 //表示下溢
#define NotPresent 4 //表示元素不存在
#define Duplicate 5 //表示有重复元素
typedef int ElemType;
typedef int Status;
//邻接表的结构体定义
typedef struct ENode{
int adjVex; //任意顶点u相邻的顶点
ElemType w; //边的权值
struct ENode *nextArc; //指向下一个边结点
}ENode;
typedef struct{
int n; //图的当前顶点数
int e; //图的当前边数
ENode **a; //指向一维指针数组
}LGraph;
//循环队列的结构体定义
typedef struct{
int front;
int rear;
int maxSize; //最大容量
ElemType *element;
}Queue;
//创建一个能容纳mSize个单元的空队列
void Create(Queue *Q,int mSize){
Q->maxSize=mSize;
Q->element=(ElemType*)malloc(sizeof(ElemType)*mSize);
Q->front=Q->rear=0;
}
//判断队列是否为空,若是,则返回TRUE;否则返回FALSE
BOOL IsEmpty(Queue *Q){
return Q->front==Q->rear;
}
//判断队列是否已满,若是,则返回TRUE,否则返回FALSE
BOOL IsFULL(Queue *Q){
return (Q->rear+1)%Q->maxSize==Q->front;
}
//获取队头元素,并通过x返回.若操作成功,则返回TRUE,否则返回FALSE
BOOL Front(Queue *Q,ElemType *x){
if(IsEmpty(Q)) //空队列处理
return FALSE;
*x=Q->element[(Q->front+1)%Q->maxSize];
return TRUE;
}
//入队.在队列Q的队尾插入元素x(入队操作)。操作成功,则返回TRUE,否则返回FALSE
BOOL EnQueue(Queue *Q,ElemType x){
if(IsFULL(Q)) //溢出处理
return FALSE;
Q->rear=(Q->rear+1)%Q->maxSize;
Q->element[Q->rear]=x;
return TRUE;
}
//出队.从队列Q中删除队头元素(出队操作)。操作成功,则返回TRUE,否则返回FALSE
BOOL DeQueue(Queue *Q){
if(IsEmpty(Q)){ //空队列处理
return FALSE;
}
Q->front=(Q->front+1)%Q->maxSize;
return TRUE;
}
//邻接表的初始化
Status Init(LGraph *lg,int nSize){
int i;
lg->n = nSize;
lg->e = 0;
lg->a = (ENode**)malloc(nSize*sizeof(ENode*)); //动态生成长度为n的一维指针数组
if(!lg->a) return ERROR;
else{
for(i = 0;i < lg->n;i ++){
lg->a[i] = NULL; //将指针数组a置空
}
return OK;
}
}
//邻接表的搜索边
Status Exist(LGraph *lg,int u,int v){
ENode *p;
if(u < 0||v < 0||u > lg->n-1||v > lg->n-1 ||u == v) return ERROR;
p = lg->a[u]; //指针p指向顶点u的单链表的第一个边结点
while(p && p->adjVex != v){
p = p->nextArc;
}
if(!p) return ERROR; //若未找到此边,则返回ERROR
else return OK;
}
//邻接表的插入边
Status Insert(LGraph *lg,int u,int v,ElemType w){
ENode *p;
if(u < 0||v < 0||u > lg->n-1||v > lg->n-1 ||u == v) return ERROR;
if(Exist(lg,u,v)) return Duplicate; //此边已存在,返回错误
p = (ENode*)malloc(sizeof(ENode)); //为新的边结点分配存储空间
p->adjVex = v;
p->w = w;
p -> nextArc = lg->a[u]; //将新的边结点插入单链表的最前面
lg->a[u] = p;
lg->e ++; //边加1
return OK;
}
//邻接表的单一顶点DFS
void DFS(int v,int visited[],LGraph g){
ENode *w;
printf("%d ",v); //访问顶点v
visited[v] = 1; //为顶点v打上访问标记
for(w = g.a[v];w;w = w->nextArc){ //遍历v的邻接点
if(!visited[w->adjVex]){
DFS(w->adjVex,visited,g); //若w未被访问,则递归调用DFS
}
}
}
//邻接表的全图DFS
void DFSGraph(LGraph g){
int i;
int *visited = (int*)malloc(g.n * sizeof(int)); //动态生成标记数组visted
for(i = 0;i < g.n;i ++){
visited[i] = 0; //visted数组初始化
}
for(i = 0;i < g.n;i ++){ //逐一检查每个顶点,若未被访问,则调用DFS
if(!visited[i]){
DFS(i,visited,g);
}
}
free(visited); //释放visted数组
}
//邻接表的单一顶点BFS
void BFS(int v,int visited[],LGraph g){
ENode *w;
Queue q;
Create(&q,g.n); //初始化队列
visited[v] = 1; //为顶点v打上访问标记
printf("%d ",v); //访问顶点v
EnQueue(&q,v); //将顶点v放入队列
while(!IsEmpty(&q)){
Front(&q,&v);
DeQueue(&q); //队首顶点出队列
for(w = g.a[v];w;w = w->nextArc){ //遍历v的所有邻接点
if(!visited[w->adjVex]){ //若w未被访问,则将其访问并放入队列
visited[w->adjVex] = 1;
printf("%d ",w->adjVex);
EnQueue(&q,w->adjVex);
}
}
}
}
//邻接表的全图BFS
void BFSGraph(LGraph g){
int i;
int *visited = (int*)malloc(g.n * sizeof(int)); //动态生成visited数组
for(i = 0;i < g.n;i ++){ //初始化visited数组
visited[i] = 0;
}
for(i = 0 ;i < g.n;i ++){ //逐一检查每个顶点,若未被访问,则调用BFS
if(!visited[i]){
BFS(i,visited,g);
}
}
free(visited);
}
void OutPut(LGraph g)
{
int i;
ENode *p;
for (i = 0; i < g.n;i++)
{
printf("%d ",i);
p = g.a[i];
for (p; p ;p = p->nextArc)
{
printf("-->%2d|%2d ",p->adjVex,p->w);
}
printf("\n");
}
}
int main(){
LGraph g;
int i,u,v,enode,edge;
ElemType w;
// printf("Please enter the number of the ENodes:");
// scanf("%d",&enode);
// Init(&g,enode);
// printf("Please enter the number of the edges:");
// scanf("%d",&edge);
// printf("Now init the graph.\n");
// for(i = 0;i < edge;i ++){
// printf("Please enter the edge:");
// scanf("%d%d%d",&u,&v,&w);
// Insert(&g,u,v,w);
// }
enode = 6;
edge = 10;
Init(&g,enode);
Insert(&g,0,1,50);
Insert(&g,0,2,10);
Insert(&g,0,4,80);
Insert(&g,1,2,15);
Insert(&g,1,4,20);
Insert(&g,2,3,15);
Insert(&g,3,1,20);
Insert(&g,3,4,45);
Insert(&g,5,3,9);
Insert(&g,5,4,10);
printf("\n\n The adjacency list is:\n\n");
OutPut(g);
printf("\n DFS:\n");
DFSGraph(g);
printf("\n\n BFS:\n");
BFSGraph(g);
// system("pause");
return 0;
}
3.最佳路径选择问题
编写程序,实现智能交通中的最佳路径选择:设有n个地点,编号为0~n-1,m条路径的起点、终点和代价由用户输入提供,采用上述邻接表作为存储结构,寻找最佳路径方案(如花费时间最少、路径长度最短、交通费用最小等,任选其一即可)
源码:
#include<stdio.h>
#include<stdlib.h>
#include <windows.h>
#define ERROR 0
#define OK 1
#define Overflow 2 //表示上溢
#define Underflow 3 //表示下溢
#define NotPresent 4 //表示元素不存在
#define Duplicate 5 //表示有重复元素
#define INFTY 32767 //表示极大值正无穷
typedef int ElemType;
typedef int Status;
//邻接表的结构体定义
typedef struct ENode{
int adjVex; //任意顶点u相邻的顶点
ElemType w; //边的权值
struct ENode *nextArc; //指向下一个边结点
}ENode;
typedef struct{
int n; //图的当前顶点数
int e; //图的当前边数
ENode **a; //指向一维指针数组
}LGraph;
//循环队列的结构体定义
typedef struct{
int front;
int rear;
int maxSize; //最大容量
ElemType *element;
}Queue;
//创建一个能容纳mSize个单元的空队列
void Create(Queue *Q,int mSize){
Q->maxSize=mSize;
Q->element=(ElemType*)malloc(sizeof(ElemType)*mSize);
Q->front=Q->rear=0;
}
//判断队列是否为空,若是,则返回TRUE;否则返回FALSE
BOOL IsEmpty(Queue *Q){
return Q->front==Q->rear;
}
//判断队列是否已满,若是,则返回TRUE,否则返回FALSE
BOOL IsFULL(Queue *Q){
return (Q->rear+1)%Q->maxSize==Q->front;
}
//获取队头元素,并通过x返回.若操作成功,则返回TRUE,否则返回FALSE
BOOL Front(Queue *Q,ElemType *x){
if(IsEmpty(Q)) //空队列处理
return FALSE;
*x=Q->element[(Q->front+1)%Q->maxSize];
return TRUE;
}
//入队.在队列Q的队尾插入元素x(入队操作)。操作成功,则返回TRUE,否则返回FALSE
BOOL EnQueue(Queue *Q,ElemType x){
if(IsFULL(Q)) //溢出处理
return FALSE;
Q->rear=(Q->rear+1)%Q->maxSize;
Q->element[Q->rear]=x;
return TRUE;
}
//出队.从队列Q中删除队头元素(出队操作)。操作成功,则返回TRUE,否则返回FALSE
BOOL DeQueue(Queue *Q){
if(IsEmpty(Q)){ //空队列处理
return FALSE;
}
Q->front=(Q->front+1)%Q->maxSize;
return TRUE;
}
//邻接表的初始化
Status Init(LGraph *lg,int nSize){
int i;
lg->n = nSize;
lg->e = 0;
lg->a = (ENode**)malloc(nSize*sizeof(ENode*)); //动态生成长度为n的一维指针数组
if(!lg->a) return ERROR;
else{
for(i = 0;i < lg->n;i ++){
lg->a[i] = NULL; //将指针数组a置空
}
return OK;
}
}
//邻接表的搜索边
Status Exist(LGraph *lg,int u,int v){
ENode *p;
if(u < 0||v < 0||u > lg->n-1||v > lg->n-1 ||u == v) return ERROR;
p = lg->a[u]; //指针p指向顶点u的单链表的第一个边结点
while(p && p->adjVex != v){
p = p->nextArc;
}
if(!p) return ERROR; //若未找到此边,则返回ERROR
else return OK;
}
//邻接表的插入边
Status Insert(LGraph *lg,int u,int v,ElemType w){
ENode *p;
if(u < 0||v < 0||u > lg->n-1||v > lg->n-1 ||u == v) return ERROR;
if(Exist(lg,u,v)) return Duplicate; //此边已存在,返回错误
p = (ENode*)malloc(sizeof(ENode)); //为新的边结点分配存储空间
p->adjVex = v;
p->w = w;
p -> nextArc = lg->a[u]; //将新的边结点插入单链表的最前面
lg->a[u] = p;
lg->e ++; //边加1
return OK;
}
int Choose(int *d, int *s,int n) //选出最小的d[i],将i加入S,i∈V-S
{
int i,minpos,min;
min=INFTY;
minpos=-1;
for(i=0;i<n;i++)
{
if(d[i]<min&&!s[i])
{
min=d[i];
minpos=i;
}
}
return minpos;
}
Status Dijkstra(int v,int *d,int *path,LGraph *lg)//迪杰斯特拉算法求路径
{
int i,j,k,w;
int distance = 0;
ENode *p;
p=lg->a[v];//工作指针
int *s;
if(v<0||v>lg->n-1)
{
return ERROR;
}
s=(int*)malloc(sizeof(int)*lg->n);
for(i=0;i<lg->n ;i++)
{
s[i]=0;
path[i]=-1;
d[i]=INFTY;
}
while(p)//初始化
{
d[p->adjVex ]=p->w ;
if(p->adjVex!=v&&d[p->adjVex ]<INFTY)
{
path[p->adjVex ]=v;
}
p=p->nextArc ;
} //对各个数组初始化
s[v]=1;
d[v]=0;
for(i=1;i<lg->n ;i++)
{
k=Choose(d,s,lg->n );
if(k==-1)
{
continue;
} //判断是否选择了有效结点
s[k]=1;
p=lg->a[k];
if(p==NULL)
{
continue ;
}
while(p)
{
if(!s[p->adjVex ]&&d[k]+p->w <d[p->adjVex ])//更新d和path
{
d[p->adjVex ]=d[k]+p->w ;
path[p->adjVex ]=k;
// distance = d[p->adjVex];
}
p=p->nextArc ;
}
}
return OK;
}
void OutPut(LGraph *lg)//此函数用于输出路径
{
int u,v;
printf("\nplease input the origin (u) and destination (v):\n");
scanf("%d %d",&u,&v);
int d[lg->n];
int path[lg->n];
Dijkstra(u,d,path,lg);
printf("The shortest path length between %d and %d is: %d\n",u,v,d[v]);
printf("\nThe path detail: ");
if (path[v] == -1)
{
printf(" Not exist!\n");
return;
}
while (path[v]!=-1)
{
printf("%d <-- ",v);
v=path[v];
}
printf("%d\n",u);
}
int main(){
LGraph g;
int nSize,edge,u,v,i;
int d[100];
int path[100];
ElemType w;
printf("Please enter the size of the mgraph: ");
scanf("%d",&nSize);
Init(&g,nSize);
printf("Please enter the number of the edges: ");
scanf("%d",&edge);
printf("\n");
for(i = 0;i < edge;i ++){
printf("Please enter the %d edge: ",i);
scanf("%d%d%d",&u,&v,&w);
Insert(&g,u,v,w);
}
// nSize = 6;
// edge = 10;
// Init(&g,nSize);
// Insert(&g,0,1,50);
// Insert(&g,0,2,10);
// Insert(&g,0,4,80);
// Insert(&g,1,2,15);
// Insert(&g,1,4,20);
// Insert(&g,2,3,15);
// Insert(&g,3,1,20);
// Insert(&g,3,4,45);
// Insert(&g,5,3,9);
// Insert(&g,5,4,10);
Dijkstra(0,d,path,&g);
OutPut(&g);
// system("pause");
return 0;
}
实验四
各种内排序算法的实现和性能比较
1.已知待排序序列以顺序表存储,数据元素以及表结构定义如下:
typedef struct entry //数据元素
{
KeyType key; //排序关键词,KeyType应该为可以比较类型
DataType data; //data包含数据元素中的其他数据项
} Entry;
typedef struct list //顺序表
{
int n; //待排序数据元素数量
Entry D[MaxSize]; //静态数组存储数据元素
} List;
参照程序10.1~10.7,编写算法,分别实现顺序表的简单选择排序、直接插入排序、冒泡排序、快速排序、两路合并排序以及堆排序。
2.编写算法,利用随机函数,在文件中随机产生n个关键字(关键字定义为整型数据)。
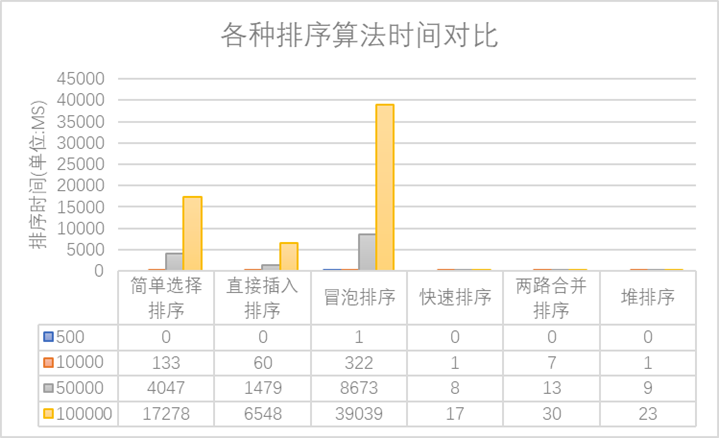
3.编写程序,分别验证简单选择排序、直接插入排序、冒泡排序、快速排序、两路合并排序以及堆排序,在待排关键字个数为500、10000、50000、100000时,完成排序所需要的时间(单位:毫秒)
4.将排序结果存放于Excel工作表中,并以图表(簇状柱形图)的方式显示。
源码:
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#include <windows.h>
#define MaxSize 50000
typedef int KeyType;
typedef int DataType;
typedef struct entry //数据元素
{
KeyType key; //排序关键词,KeyType应该为可以比较类型
DataType data; //data包含数据元素中的其他数据项
} Entry;
typedef struct list //顺序表
{
int n; //待排序数据元素数量
Entry D[MaxSize]; //静态数组存储数据元素
} List;
//简单选择排序算法
int FindMin(List list,int StartIndex) //在startIndex至表尾范围内找到最小关键字元素下标
{
int MInIndex = StartIndex;
int i;
for (i = StartIndex+1; i < list.n;i++)
{
if(list.D[i].key<list.D[MInIndex].key)
{
MInIndex = i;
}
}
return MInIndex;
}
void Swap(Entry *D ,int i,int j) //交换顺序表中两元素位置
{
Entry temp;
if(i==j)
return;
temp = *(D + i);
*(D + i) = *(D+j);
*(D + j) = temp;
}
void SelectSort(List *list)
{
int i,MinIndex;
int StartIndex = 0;
// for (i = 0; i < list->n;i++)
// {
// MinIndex=FindMin(*list, StartIndex);
// Swap(list->D, i, MinIndex);
// StartIndex++;
// }
while(StartIndex<list->n)
{
MinIndex=FindMin(*list, StartIndex);
Swap(list->D, StartIndex, MinIndex);
StartIndex++;
}
}
//直接插入排序
void InsertSort(List *list)
{
int i, j; //i为待插入元素下标
for (i = 1; i < list->n; i++) //每一趟待插入元素
{
Entry insertItem = list->D[i];
for (j = i - 1; j >= 0; j--)
{ //不断将有序序列中元素向后移动,为待插入元素空出一个位置
if (insertItem.key < list->D[j].key)
list->D[j + 1] = list->D[j];
else break;
}
list->D[j + 1] = insertItem; //待插入元素有序存放至有序序列中
}
}
//冒泡排序
void BubbleSort(List* list)
{
int i, j; //i标识每趟排序范围最后一个元素下标,每趟排序元素下标范围是0~i
bool isSwap = false; //标记一趟排序中是否发生了元素交换
for (i =list->n - 1; i > 0; i--)
{
for (j = 0; j < i; j++)
{
if (list->D[j].key > list->D[j + 1].key)
{
Swap(list->D, j, j + 1);
isSwap = true;
}
}
if (!isSwap) break; //如果本趟排序没有发生元素交换,排序完成
}
}
//划分
int Partition(List *list,int low,int high)
{
int i = low, j = j = high + 1; //注意是high+1
Entry pivot = list->D[low]; //pivot是分划元素
do
{
do
{
i++;
} while (i<=high && list->D[i].key<pivot.key);
do
{
j--;
} while (list->D[j].key>pivot.key);
if(i<j)
Swap(list->D,i,j); //若i<j,交换D[i]与D[j]
} while (i<j);
Swap(list->D,low,j); //若i>=j,交换D[low]与D[j]
return j;
}
//快速排序的递归函数
void QuickSort(List *list,int low ,int high)
{
int k;
if(low<high)
{
k = Partition(list,low,high);
QuickSort(list,low,k-1); //递归排序(low,k-1)
QuickSort(list,k+1,high); //递归排序(k+1,high)
}
}
//快速排序的主调用函数
void QuickSort(List *list)
{
QuickSort(list,0,list->n-1);
}
void Merge(List *list,int left,int mid,int right)
{
int *Temp = new int[right - left + 1];
// int *Temp = (int *)malloc(sizeof(int)*list->n);
int i = left, j = mid + 1, k = 0;
while((i<=mid)&&(j<=right))
{ //每次把比较小的放进Temp里
if(list->D[i].key<=list->D[j].key)
Temp[k++] = list->D[i++].key;
else
Temp[k++] = list->D[j++].key;
}
while(i<=mid) Temp[k++] = list->D[i++].key; //将剩余元素复制到Temp
while(j<=right) Temp[k++] = list->D[j++].key;
for (i = 0, k = left; k <= right;)
list->D[k++].key = Temp[i++];
}
//快速排序的递归函数
void MergeSort(List *list,int left,int right)
{
if(left<right)
{
int mid = left + (right-left) / 2; //二分选择中间值
MergeSort(list,left, mid); //递归排序左半部分
MergeSort(list, mid + 1, right); //递归排序右半部分
Merge(list,left,mid,right); //合并左右两部分
}
}
//快速排序的主调用函数
void MergeSort(List *list)
{
MergeSort(list,0,list->n-1);
}
//最大堆结构体
typedef struct maxheap
{
int n;
Entry D[MaxSize];
} MaxHeap;
//向下调整
void AdjustDown(Entry heap[],int current,int border)
{
int p = current;
int maxChild;
Entry temp;
while(2*p+1<=border)
{
if((2*p+2<=border) &&(heap[2*p+1].key < heap[2*p+2].key))
maxChild = 2 * p + 2;
else
maxChild = 2 * p + 1;
if(heap[p].key>=heap[maxChild].key)
break;
else //否则将p和其最大孩子交换
{
temp = heap[p];
heap[p] = heap[maxChild];
heap[maxChild] = temp;
p = maxChild;
}
}
}
void HeapSort(MaxHeap *hp)
{
int i;
Entry temp;
for (i =( hp->n -2) / 2; i >= 0;i--)
{
AdjustDown(hp->D,i,hp->n-1);
}
for (i = hp->n - 1; i >= 0; i--) //i指向当前堆的堆底元素
{
Swap(hp->D, 0, i); //交换堆底与堆顶元素
AdjustDown(hp->D, 0, i - 1);
}
}
void Rand(List *list1)
{
int i;
srand((unsigned int)time(NULL)); //以运行程序时的时间作为随机数种子
for (i = 0; i <list1->n ; i++)
{
list1->D[i].key = rand();
}
}
void Output(List *list)
{
int i;
for (i = 0; i < list->n; i++)
{
printf("%4d ",list->D[i].key);
}
}
void Output2(MaxHeap *heap)
{
int i;
for (i = 0; i < heap->n; i++)
{
printf("%4d ",heap->D[i].key);
}
}
MaxHeap heap;
int main()
{
List list;
// MaxHeap heap;
static List temp=list;
int i;
clock_t start, finish;
double duration;
list.n = MaxSize;
printf("numbers: %d \n",MaxSize);
Rand(&list); //初始化
// printf("Initial list:\n");
// Output(&list); //输出
temp = list;
// printf("\n");
start = clock();
SelectSort(&list);
finish = clock();
duration=(double)(finish - start) ;
// printf("\n\nSelectSort:\n");
// printf( "%f ms\n", duration); //精度是1ms //显示排序时间
Output(&list);
list = temp;
// printf("\n\nInitial list:\n");
// Output(&temp);
// printf("\nInsertSort:\n");
start = clock();
InsertSort(&list);
finish = clock();
duration=(double)(finish - start) / CLOCKS_PER_SEC;
// printf("\n\nInsertSort:\n");
// printf( "%f ms\n", duration*1000 );
Output(&list);
list = temp;
// printf("\n\nInitial list:\n");
// Output(&temp);
// printf("\nBubbleSort:\n");
start = clock();
BubbleSort(&list);
finish = clock();
duration=(double)(finish - start) / CLOCKS_PER_SEC;
// printf("\n\nBubbleSort:\n");
// printf( "%f ms\n", duration*1000 );
Output(&list);
list = temp;
// printf("\n\nInitial list:\n");
// Output(&temp);
// printf("\nQuickSort:\n");
start = clock();
QuickSort(&list);
finish = clock();
duration=(double)(finish - start) / CLOCKS_PER_SEC;
// printf("\n\nQuickSort:\n");
// printf( "%f ms\n", duration*1000 );
Output(&list);
list = temp;
// printf("\n\nInitial list:\n");
// Output(&temp);
// printf("\nMergeSort:\n");
start = clock();
MergeSort(&list);
finish = clock();
duration=(double)(finish - start) / CLOCKS_PER_SEC;
// printf("\n\nMergeSort:\n");
// printf( "%f ms\n", duration*1000 );
Output(&list);
list = temp;
heap.n = list.n;
for (i = 0; i < list.n;i++)
{
heap.D[i].key = list.D[i].key;
}
// printf("\n\nInitial list:\n");
// Output(&temp);
// printf("\nHeapSort:\n");
start = clock();
HeapSort(&heap);
finish = clock();
duration=(double)(finish - start) / CLOCKS_PER_SEC;
// printf("\n\nHeapSort:\n");
// printf( "%f ms\n", duration*1000 );
Output2(&heap);
}
时间统计与比较