LeetCode刷题记录

分享｜如何科学刷题？- 讨论 - 力扣（LeetCode）

链表

21《合并两个有序链表》

思路

• 建一个哑结点 dummy，方便统一处理首节点。
• 用 cur 指向当前已合并部分的最后一个节点。
• 当 l1、l2 均非空时，比较两节点值：
  • 较小者接到 cur.next，对应链表指针前进一步。
  cur 也前进一步。
• 退出循环后，必有一条链已空，直接把另一条剩余部分一次挂到 cur.next。
• 返回 dummy.next（真正的头结点）。

代码

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
    public ListNode mergeTwoLists(ListNode list1, ListNode list2) {
        ListNode dummy = new ListNode();
        ListNode cur = dummy;
        ListNode l1 = list1;
        ListNode l2 = list2;
        while(l1!=null && l2!=null){
            if(l1.val<=l2.val){
                cur.next = l1;
                l1 = l1.next;
            }else{
                cur.next = l2;
                l2 = l2.next;
            }
            cur = cur.next;
        }
        if(l1!=null) cur.next = l1;
        if(l2!=null) cur.next = l2;
        return dummy.next;
    }
}

复杂度

时间：只遍历每个节点一次，O(m+n)，m、n 分别为两链表长度。
空间：只用了几个指针变量，O(1)（输出链表不计入额外空间）。

---

易错点

易错点	正确做法	备注
while 条件写成 `		`
循环体内忘了移动 cur	每次接完节点后 cur = cur.next	否则链表会断
最后只处理 l1 != null 而漏掉 l2	if (l1 != null) cur.next = l1; 之后再写 else if (l2 != null)... 或直接两条独立 if	因为只有一个会非空，但保险写法是两条 if
忘记返回 dummy.next	千万别 return dummy	dummy 是哨兵，真实头结点是 dummy.next

2《两数相加》

思路

• 建一个哑结点 dummy，统一处理结果链表的首节点。
• 用 cur 指向当前结果链表的最后一个节点，初始指向 dummy。
• 维护一个整型变量 carry 记录进位，初始为 0。
• 只要 l1、l2 还有节点 或 carry ≠ 0，就继续循环：
  • 取出 l1、l2 当前节点的值（若节点为空则用 0 补位）。
  • 计算 sum = 两节点值 + carry。
  • 新建节点 new ListNode(sum % 10) 接到 cur.next。
  • 更新 carry = sum / 10。
  • cur 前进一步；l1、l2 若不为空也前进一步。
• 循环结束后所有位（包括最高位进位）均已生成，返回 dummy.next。

代码

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
    public ListNode addTwoNumbers(ListNode l1, ListNode l2) {
        // 1. 哨兵节点，简化头结点处理
        ListNode dummy = new ListNode();
        ListNode cur   = dummy;

        int carry = 0;              // 2. 进位标志，初始为 0

        // 3. 只要任一链表还有节点，或仍有进位，就继续
        while (l1 != null || l2 != null || carry != 0) {
            int v1 = (l1 == null) ? 0 : l1.val;   // 取当前位，空则补 0
            int v2 = (l2 == null) ? 0 : l2.val;

            int sum   = v1 + v2 + carry;          // 4. 当前位 + 进位
            carry     = sum / 10;                 // 5. 更新进位
            cur.next  = new ListNode(sum % 10);   // 6. 新建节点保存个位
            cur       = cur.next;                 // 7. 推进结果指针

            // 8. 两链表指针同步前进
            if (l1 != null) l1 = l1.next;
            if (l2 != null) l2 = l2.next;
        }

        return dummy.next;   // 9. 哨兵的下一个节点才是头结点
    }
}

复杂度

维度	结论	说明
时间复杂度	O(max(m, n))	每个节点最多遍历一次
空间复杂度	O(max(m, n))	新建链表长度最多 max(m, n)+1

易错点

易错点	正确姿势
直接 cur.next.val = ...	必须先 new ListNode(...) 再赋值
忘记维护 carry	每轮更新 carry = sum / 10
循环条件仅写 l1 != null && l2 != null	需包含 carry != 0，否则最高位进位会漏
剩余节点直接拼接	剩余节点仍需逐位加 carry
返回 dummy	应返回 dummy.next

TODO 两数相加2

206《反转链表》

思路

参考206. 反转链表 - 力扣（LeetCode）

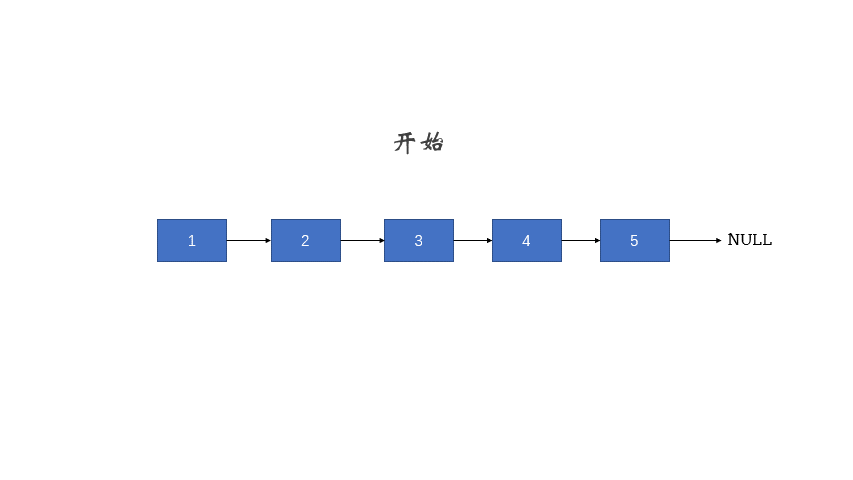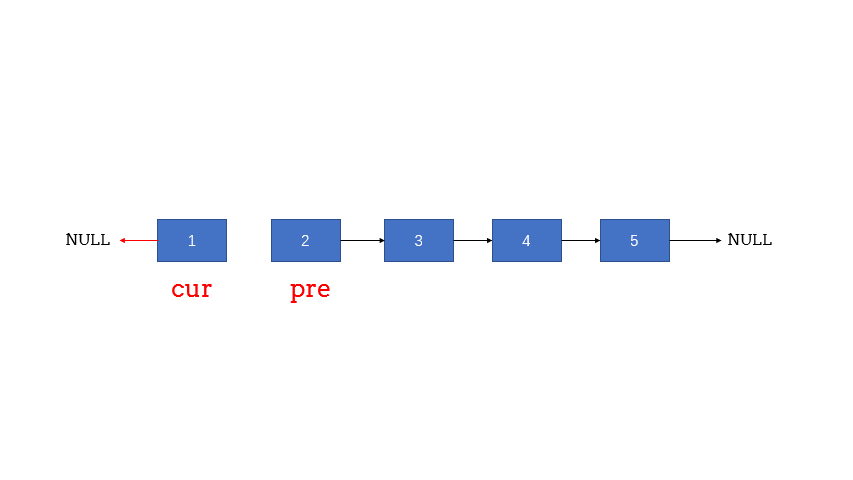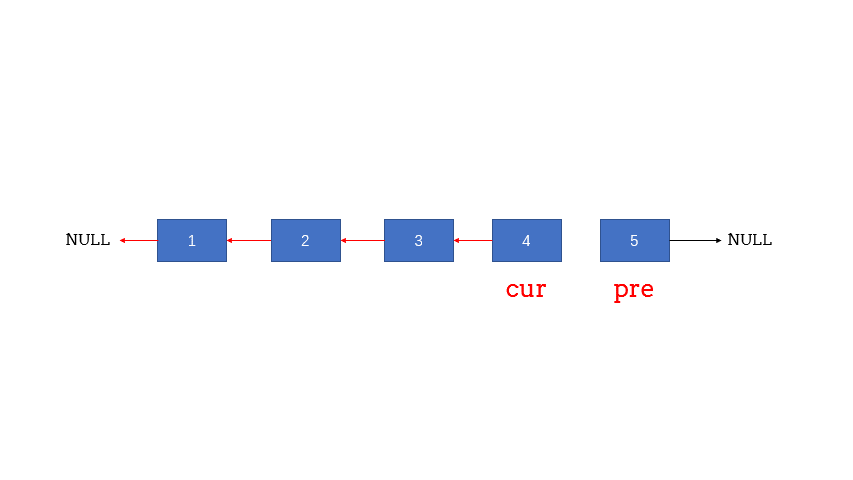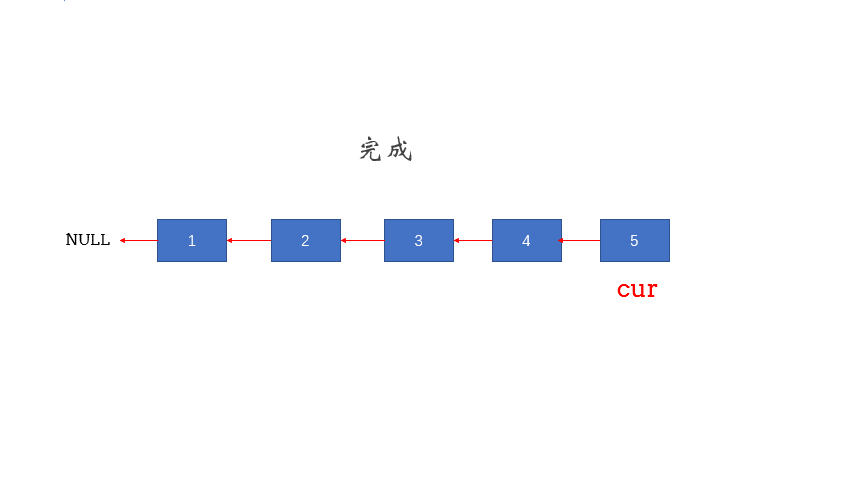
• 定义两个指针： pre 和 cur ；pre 在前 cur 在后。
• 每次让 pre 的 next 指向 cur ，实现一次局部反转
• 局部反转完成之后，pre 和 cur 同时往前移动一个位置
• 循环上述过程，直至 pre 到达链表尾部

代码

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
    public ListNode reverseList(ListNode head) {
        ListNode pre = null;   // 已反转部分的头结点
        ListNode cur = head;   // 当前待反转节点
        ListNode tmp = null;   // 临时保存 cur 的下一个节点
        while (cur != null) {
            tmp = cur.next;    // 1. 先保存下一节点
            cur.next = pre;    // 2. 反转指针
            pre = cur;         // 3. pre 前进一步
            cur = tmp;         // 4. cur 前进一步
        }
        return pre;            // 5. pre 指向新头结点  
        //当 cur 变为 null，意味着链表已经遍历完了，pre 此时指向的是新链表的头节点
    }
}

复杂度

维度	结论	说明
时间复杂度	O(n)	每个节点仅访问一次
空间复杂度	O(1)	仅用常数级指针变量，原地反转

易错点

易错点	正确姿势
忘记保存 cur.next	先用 tmp = cur.next 暂存
返回 cur 而非 pre	循环结束时 cur == null，应返回 pre
修改指针顺序错误	必须“先存 next，再反转，再移动双指针”
未处理空链表	当 head == null 时直接返回 null 即可（代码已隐含）

92《反转链表 II》

思路

• 建一个哑结点 dummy，指向原头结点，方便处理 left = 1 时头结点也会反转的场景。
• 用 p1 指向待反转区间的前驱节点：
  • 从 dummy 出发，走 left-1 步即可到达。
• 用 start 指向待反转区间的第一个节点（p1.next）。
• 用 end 指向待反转区间的最后一个节点：
  • 从 start 出发，再向右走 right-left 步即可到达。
• 断开区间：
  • 保存 end.next 为 next，后续需要重新拼接。
  • 令 end.next = null，形成独立子链表 start→…→end。
• 反转子链表：
  • 调用 reverse(start)，返回反转后的新头 newHead。
• 重新接回：
  • p1.next 指向 newHead；
  • 原 start（现反转后的尾）指向之前保存的 next。
• 返回 dummy.next 即为最终链表。

代码

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
    public ListNode reverseBetween(ListNode head, int left, int right) {
        ListNode dummy = new ListNode(-1, head);
        
        // 1. 找到 [left] 前驱 p1
        ListNode p1 = dummy;
        for (int i = 1; i < left; i++) {
            p1 = p1.next;
        }
        
        // 2. 定位反转段头 start
        ListNode start = p1.next;
        
        // 3. 找到反转段尾 end
        ListNode end = start;
        for (int i = left; i < right; i++) {
            end = end.next;
        }
        
        // 4. 断开并反转
        ListNode next = end.next;
        end.next = null;
        p1.next = reverse(start);
        
        // 5. 拼回
        start.next = next;
        
        return dummy.next;
    }

    // 通用反转链表函数
    private ListNode reverse(ListNode head) {
        ListNode cur = head;
        ListNode pre = null;
        ListNode tmp = null;
        while (cur != null) {
            tmp = cur.next;
            cur.next = pre;
            pre = cur;
            cur = tmp;
        }
        return pre;
    }
}

复杂度

维度	结论	说明
时间复杂度	O(n)	链表最多遍历两次（定位 + 反转）
空间复杂度	O(1)	仅用常数级指针变量，原地反转

易错点

易错点	正确姿势
未使用哑结点	使用 dummy，方便处理 left = 1 的情况
未保存 end.next	反转前先用变量保存，否则后续无法正确拼接链表
反转后忘记把原 start 接到剩余链表	start.next = next 必须在反转后执行
返回 head 而非 dummy.next	头结点可能已变更，应返回 dummy.next
reverse 函数忘记返回新头	反转后返回 pre，即新头结点

24《两两交换链表节点》

思路

• 建一个哑结点 dummy，指向原头结点，方便处理头结点本身要被交换的场景。
• 用 pre 指向已交换部分的最后一个节点，初始指向 dummy。
• 用 cur 指向当前待交换对的第一个节点，初始指向 head。
• 只要 cur 和 cur.next 均非空，就继续循环：
  • 用 nxt 保存 cur.next（即当前对的第二个节点）。
  • pre.next 指向 nxt，把 nxt 提前到 cur 前面。
  • cur.next 指向 nxt.next，把 cur 接到下一对的头部。
  • nxt.next 指向 cur，完成本对交换。
  • pre 移动到 cur（已交换对的末尾）。
  • cur 移动到 cur.next（下一对的第一个节点）。
• 循环结束后所有相邻节点均已两两交换，返回 dummy.next。

代码

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
    public ListNode swapPairs(ListNode head) {
        ListNode dummy = new ListNode(0, head);
        ListNode pre = dummy;
        ListNode cur = head;

        while (cur != null && cur.next != null) {
            ListNode nxt = cur.next;

            pre.next = nxt;        // 1. pre 指向第二个节点
            cur.next = nxt.next;   // 2. 第一个节点指向下一对的头
            nxt.next = cur;        // 3. 第二个节点指向第一个节点

            pre = cur;             // 4. pre 移动到已交换对的末尾
            cur = cur.next;        // 5. cur 移动到下一对的头
        }
        return dummy.next;
    }
}

复杂度

维度	结论	说明
时间复杂度	O(n)	每个节点只遍历一次
空间复杂度	O(1)	仅用常数级指针变量，原地交换

易错点

易错点	正确姿势
未使用哑结点	使用 dummy 处理头结点交换
交换后未移动 cur	每轮末尾必须 cur = cur.next
指针顺序写反	严格按照 pre→nxt→cur→nextPair 顺序调整
返回 head 而非 dummy.next	头结点可能已变更，应返回 dummy.next

25《K 个一组翻转链表》

思路

• 建一个哑结点 dummy，指向原头结点，方便处理 k 整除头结点的情况。
• 用 pre 指向已翻转部分的最后一个节点，初始指向 dummy。
• 用 end 作为滑动窗口的右端，初始也指向 dummy。
• 只要 end.next 非空，就继续：
  • 让 end 先走 k 步，若中途遇到 null，说明剩余不足 k，直接返回。
  • 保存当前段头结点 start = pre.next。
  • 保存后一段头结点 tmp = end.next。
  • 断开当前段：end.next = null。
  • 翻转 start 到 end 的子链表，返回新头 newHead。
  • 重新拼接：pre.next = newHead，start.next = tmp。
  • pre 和 end 都移动到 start（当前段的末尾）。
• 循环结束后整个链表分段翻转完成，返回 dummy.next。

代码

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
    public ListNode reverseKGroup(ListNode head, int k) {
        ListNode dummy = new ListNode(0, head);
        ListNode pre = dummy;
        ListNode end = dummy;

        while (end.next != null) {
            // 1. end 先走 k 步
            for (int i = 0; i < k && end != null; i++) {
                end = end.next;
            }
            if (end == null) break;  // 剩余不足 k

            // 2. 保存关键节点
            ListNode start = pre.next;
            ListNode tmp = end.next;

            // 3. 断开 & 翻转
            end.next = null;
            pre.next = reverse(start);
            start.next = tmp;

            // 4. 更新 pre & end 到下一组起点前
            pre = start;
            end = start;
        }
        return dummy.next;
    }

    // 通用翻转函数
    private ListNode reverse(ListNode head) {
        ListNode cur = head;
        ListNode pre = null;
        ListNode tmp = null;
        while (cur != null) {
            tmp = cur.next;
            cur.next = pre;
            pre = cur;
            cur = tmp;
        }
        return pre;
    }
}

复杂度

维度	结论	说明
时间复杂度	O(n)	每个节点至多遍历两次（定位 + 反转）
空间复杂度	O(1)	仅用常数级指针变量

易错点

易错点	正确姿势
未检测剩余节点是否够 k	用 end 先走 k 步，为 null 即跳出循环
翻转后未正确拼接前后两段	保存 start、tmp 并正确连接
pre/end 未移动到当前段末尾	翻转后 pre = end = start
循环条件写成 end != null	用 end.next != null 可提前终止无效遍历
reverse 函数忘记返回新头	返回 pre，即翻转后的头结点

变体

最后一组不足k个也进行反转

为了在剩余节点不足 k 个时也进行反转，我们只需要修改处理这个“剩余部分”的逻辑。

当前，if (end == null) break; 这条语句直接放弃了对剩余部分的处理。我们要做的是，在 while 循环结束时，对剩下的那部分链表（无论其长度如何）执行一次反转操作。

while 循环结束后：

• pre 指针正位于上一个被反转分组的末尾节点（或者，如果从未进行过反转，则 pre 仍然是 dummy 节点）。
• pre.next 指向的是剩余部分的头节点。

因此，我们只需要在 while 循环之后，对 pre.next 开始的链表进行一次反转即可。这只需要在 while 循环外添加一行代码。只需要再while 循环之后、return 语句之前，增加了一行 pre.next = reverse(pre.next);。

/**
 * Definition for singly-linked list.
 * public class ListNode {
 * int val;
 * ListNode next;
 * ListNode() {}
 * ListNode(int val) { this.val = val; }
 * ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
    public ListNode reverseKGroup(ListNode head, int k) {
        ListNode dummy = new ListNode(0, head);
        ListNode pre = dummy;
        ListNode end = dummy;

        while (end.next != null) {
            // 1. end 先走 k 步
            for (int i = 0; i < k && end != null; i++) {
                end = end.next;
            }
            if (end == null) {
                // 剩余不足 k 个，跳出循环，后续统一处理
                break;
            }

            // 2. 保存关键节点
            ListNode start = pre.next;
            ListNode tmp = end.next;

            // 3. 断开 & 翻转
            end.next = null;
            pre.next = reverse(start);
            start.next = tmp;

            // 4. 更新 pre & end 到下一组起点前
            pre = start;
            end = start;
        }

        // ***** 唯一的修改 *****
        // 循环结束后，pre 指向最后一个完整翻转组的尾部
        // pre.next 指向剩余部分的头部，直接翻转剩余部分
        pre.next = reverse(pre.next);

        return dummy.next;
    }

    // 通用翻转函数 (无需修改)
    private ListNode reverse(ListNode head) {
        ListNode cur = head;
        ListNode pre = null;
        ListNode tmp = null;
        while (cur != null) {
            tmp = cur.next;
            cur.next = pre;
            pre = cur;
            cur = tmp;
        }
        return pre;
    }
}

仅反转奇数组 / 偶数组

核心思路：

1. 引入计数器：在 while 循环外初始化一个计数器，例如 int groupIndex = 1;。
2. 条件性反转：在 while 循环内部，当我们成功找到一个完整的 k 元素分组后，检查 groupIndex 的值。
   • 如果需要反转奇数组，就在 groupIndex 为奇数时执行反转逻辑。
   • 如果需要反转偶数组，就在 groupIndex 为偶数时执行反转逻辑。
3. 更新指针：
   • 如果执行了反转：pre 指针的更新方式不变，移动到反转后分组的末尾（即原来的 start 节点）。
   • 如果未执行反转：我们必须手动将 pre 指针移动到这个未反转分组的末尾（即 end 节点），为下一次迭代做准备。
4. 递增计数器：在每次循环（无论是否反转）结束时，将 groupIndex 加一。

class Solution {
    public ListNode reverseOddKGroups(ListNode head, int k) {
        if (head == null || k <= 1) {
            return head;
        }
        
        ListNode dummy = new ListNode(0, head);
        ListNode pre = dummy;
        ListNode end = dummy;
        int groupIndex = 1; // 分组计数器，从 1 开始

        while (true) {
            // 1. end 先走 k 步，找到当前组的尾部
            for (int i = 0; i < k && end != null; i++) {
                end = end.next;
            }
            // 如果 end 为 null，说明剩余节点不足 k 个，或刚好处理完
            if (end == null) {
                break;
            }

            // 2. 根据 groupIndex 的奇偶性决定是否反转
            ListNode start = pre.next;
            
            if (groupIndex % 2 == 1) { // 是奇数组，执行反转
                ListNode nextGroupStart = end.next;
                end.next = null; // 断开链表
                pre.next = reverse(start); // 反转并连接
                start.next = nextGroupStart; // 连接回剩余部分
                
                // 更新 pre 指针到反转后分组的末尾（即原 start 节点）
                pre = start;
            } else { // 是偶数组，不反转，直接跳到该组末尾
                pre = end;
            }
            
            // 3. 为下一次循环做准备
            end = pre; // 将 end 重置到 pre 的位置
            groupIndex++; // 计数器加一
        }
        return dummy.next;
    }

    // 通用反转函数 (无需修改)
    private ListNode reverse(ListNode head) {
        ListNode pre = null;
        ListNode cur = head;
        while (cur != null) {
            ListNode tmp = cur.next;
            cur.next = pre;
            pre = cur;
            cur = tmp;
        }
        return pre;
    }
}

160《链表相交节点》

思路

• 若两链表有交点，则从交点到尾部为公共部分，长度相同。
• 设链表 A 长度 a，链表 B 长度 b，公共部分长度 c。
• 让双指针 l1、l2 分别从 headA、headB 出发：
  • 走到尾后立刻换到另一条链表的头继续走；
  • 两指针第二次相遇时，走过的路程均为 a + b - c，恰好在交点处相遇；
  • 若无交点，两指针最终同时为 null，返回 null 即可。
• 时间 O(a + b)，空间 O(1)。

代码

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) {
 *         val = x;
 *         next = null;
 *     }
 * }
 */
public class Solution {
    public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
        if (headA == null || headB == null) return null;

        ListNode l1 = headA;
        ListNode l2 = headB;

        // 双指针交替走，同速同终点
        while (l1 != l2) {
            l1 = (l1 == null) ? headB : l1.next;
            l2 = (l2 == null) ? headA : l2.next;
        }
        return l1; // 交点或 null
    }
}

复杂度

维度	结论	说明
时间复杂度	O(n)	n = len(A) + len(B)
空间复杂度	O(1)	仅用两个指针，无额外空间

易错点

易错点	正确姿势
循环条件写成 l1.next != l2.next	应比较节点自身 l1 != l2，否则漏判单节点交点
未处理空链表	先判空，直接返回 null
走到尾后未切换到另一条链表	用 ?: 表达式在 null 时切换链头
返回 l1.next	返回 l1 即可，无交点时同为 null

234《回文链表》

思路

• 把所有节点值顺序存入 线性容器（如 ArrayList）。
• 用双指针 left、right 分别从首尾向中间扫描：
  • 若对应值不等，立即返回 false；
  • 直至两指针交错，返回 true。
• 复杂度：时间 O(n)，空间 O(n)。

代码

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
    public boolean isPalindrome(ListNode head) {
        // 1. 顺序收集节点值
        List<Integer> vals = new ArrayList<>();
        for (ListNode p = head; p != null; p = p.next) {
            vals.add(p.val);
        }

        // 2. 双指针判回文
        int left = 0, right = vals.size() - 1;
        while (left < right) {
            if (!vals.get(left).equals(vals.get(right))) {
                return false;
            }
            left++;
            right--;
        }
        return true;
    }
}

复杂度

维度	结论	说明
时间复杂度	O(n)	遍历链表 + 双指针扫描
空间复杂度	O(n)	额外 ArrayList 存储值

易错点

易错点	正确姿势
忘记判空链表	空链表视为回文，直接返回 true
双指针比较用 ==	对包装类型使用 equals 避免装箱比较错误
双指针条件写成 <=	写 < 即可，左右相等时无需再比较
额外空间 O(n) 不满足要求	可用快慢指针+反转后半段实现 O(1)（面试进阶）

思路2

• 用 快慢指针 找到链表中间节点，把链表拆成前后两段。
• 反转后半段，得到新的头结点 head2。
• 同时遍历前半段 head 与反转后的后半段 head2：
  • 值不等 → 非回文，直接返回 false；
  • 全部相等 → 回文，返回 true。
• （如需还原链表，可再反转一次后半段并接回。）
• 时间 O(n)，空间 O(1)。

代码

class Solution {
    public boolean isPalindrome(ListNode head) {
        ListNode mid = middleNode(head);      // 1. 找中点
        ListNode head2 = reverseList(mid);    // 2. 反转后半段

        // 3. 双指针同时遍历两段
        while (head2 != null) {
            if (head.val != head2.val) return false;
            head = head.next;
            head2 = head2.next;
        }
        return true;
    }

    /** 876. 链表的中间结点 */
    private ListNode middleNode(ListNode head) {
        ListNode slow = head, fast = head;
        while (fast != null && fast.next != null) {
            slow = slow.next;
            fast = fast.next.next;
        }
        return slow;
    }

    /** 206. 反转链表 */
    private ListNode reverseList(ListNode head) {
        ListNode pre = null, cur = head;
        while (cur != null) {
            ListNode nxt = cur.next;
            cur.next = pre;
            pre = cur;
            cur = nxt;
        }
        return pre;
    }
}

复杂度

维度	结论	说明
时间复杂度	O(n)	遍历链表 3 次
空间复杂度	O(1)	仅用常数级指针变量

易错点

易错点	正确姿势
快慢指针写错	while (fast != null && fast.next != null)
反转后未同步遍历	用两个指针同时从头和尾向中间扫描
空链表未处理	空链表视为回文，直接返回 true
需要还原链表	面试时可再反转一次后半段并接回

141《环形链表》

思路

• 用 哈希表（HashSet） 记录遍历过的节点。
• 每走一步就检查当前节点是否已存在于集合中：
  • 存在 → 有环，立即返回 true；
  • 不存在 → 加入集合，继续向后。
• 走到 null 仍未重复 → 无环，返回 false。
• 时间 O(n)，空间 O(n)。

代码

/**
 * Definition for singly-linked list.
 * class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) {
 *         val = x;
 *         next = null;
 *     }
 * }
 */
public class Solution {
    public boolean hasCycle(ListNode head) {
        Set<ListNode> seen = new HashSet<>();
        ListNode cur = head;
        while (cur != null) {
            if (seen.contains(cur)) return true;
            seen.add(cur);
            cur = cur.next;
        }
        return false;
    }
}

复杂度

维度	结论	说明
时间复杂度	O(n)	每个节点最多遍历一次
空间复杂度	O(n)	哈希表存储所有节点引用

易错点

易错点	正确姿势
使用值比较	必须比较 节点对象本身
未判空链表	空链表直接返回 false
空间要求 O(1) 场景	改用快慢指针（面试高频进阶）

142《环形链表 II》

思路

• 使用 哈希表（HashSet） 顺序遍历链表。
• 每访问一个节点，先查表：
  • 若已存在 → 该节点即为 环入口，立即返回；
  • 若不存在 → 存入集合，继续后移。
• 遍历到 null 仍未重复 → 无环，返回 null。
• 时间 O(n)，空间 O(n)。

代码

/**
 * Definition for singly-linked list.
 * class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) {
 *         val = x;
 *         next = null;
 *     }
 * }
 */
public class Solution {
    public ListNode detectCycle(ListNode head) {
        Set<ListNode> seen = new HashSet<>();
        ListNode cur = head;
        while (cur != null) {
            if (seen.contains(cur)) return cur; // 环入口
            seen.add(cur);
            cur = cur.next;
        }
        return null; // 无环
    }
}

复杂度

维度	结论	说明
时间复杂度	O(n)	每个节点最多遍历一次
空间复杂度	O(n)	集合存储所有节点引用

易错点

易错点	正确姿势
仅比较节点值	必须比较 节点对象本身（地址）
未处理空链表	空链表直接返回 null
空间要求 O(1) 场景	改用快慢指针（面试高频进阶）

快慢指针（Floyd 判圈法）

• hasCycle（141）空间从 O(n) 降成 O(1)
• detectCycle（142）空间也从 O(n) 降成 O(1)

141《环形链表》——快慢指针版

public class Solution {
    public boolean hasCycle(ListNode head) {
        ListNode slow = head, fast = head;
        while (fast != null && fast.next != null) {
            slow = slow.next;
            fast = fast.next.next;
            if (slow == fast) return true; // 相遇即有环
        }
        return false;
    }
}

142《环形链表 II》——快慢指针版

public class Solution {
    public ListNode detectCycle(ListNode head) {
        ListNode slow = head, fast = head;

        // 1. 先找相遇点
        boolean hasCycle = false;
        while (fast != null && fast.next != null) {
            slow = slow.next;
            fast = fast.next.next;
            if (slow == fast) { hasCycle = true; break; }
        }
        if (!hasCycle) return null;

        // 2. 一个指针回到头，再同步走
        ListNode ptr = head;
        while (ptr != slow) {
            ptr = ptr.next;
            slow = slow.next;
        }
        return ptr; // 环入口
    }
}

复杂度对比

方案	时间	空间	说明
HashSet	O(n)	O(n)	直接、易写
快慢指针	O(n)	O(1)	面试高频、进阶要求

因此，在 O(1) 空间要求下，用快慢指针更好。

138《随机链表的复制》

思路

• 使用 哈希表 辅助，分两趟完成：
  1. 第一次遍历：顺序遍历原链表，为每个原节点创建对应的新节点，并存入 map<原节点, 新节点>。
  2. 第二次遍历：再次顺序遍历原链表，通过哈希表把新节点的 next 和 random 指针一次性映射到正确的新节点上。
• 哈希表保证 O(1) 时间定位任意旧节点对应的新节点。
• 时间 O(N)，空间 O(N)。

代码

/*
// Definition for a Node.
class Node {
    int val;
    Node next;
    Node random;

    public Node(int val) {
        this.val = val;
        this.next = null;
        this.random = null;
    }
}
*/
class Solution {
    // 时间复杂度 O(N)，空间复杂度 O(N)
    public Node copyRandomList(Node head) {
        if (head == null) return null;

        Map<Node, Node> map = new HashMap<>();
        Node curr = head;

        // 1. 第一次遍历：创建新节点并建立旧→新的映射
        while (curr != null) {
            map.put(curr, new Node(curr.val));
            curr = curr.next;
        }

        // 2. 第二次遍历：设置 next 和 random 指针
        curr = head;
        while (curr != null) {
            Node clone = map.get(curr);
            clone.next   = map.get(curr.next);   // 可为 null
            clone.random = map.get(curr.random); // 可为 null
            curr = curr.next;
        }

        return map.get(head); // 返回新链表头
    }
}

复杂度

维度	结论	说明
时间复杂度	O(N)	两次线性遍历
空间复杂度	O(N)	哈希表存储所有节点引用

易错点

易错点	正确姿势
直接复制值导致指针错乱	必须创建 新节点对象，并用哈希表做映射
next/random 指向旧节点	用 map.get(旧节点) 翻译成 新节点
未处理空链表	空链表直接返回 null
空间要求 O(1) 场景	面试追问时改用 原地复制 + 拆分 双指针技巧

148《排序链表》

思路

先快慢指针切中点 → 递归排序左右段 → 双指针合并两段有序链表。

参考：148. 排序链表 - 力扣（LeetCode）

• 自顶向下归并排序：
  1. 用 快慢指针 把链表一分为二，得到左右两段；
  2. 递归排序左右两段；
  3. 合并两个已排序链表。
• 时间复杂度 **O(n log n)**，空间复杂度 O(log n) （递归栈）。
• 整个过程中没有使用额外数组，只在原链表上断链、重连。

通过递归实现链表归并排序，有以下两个环节：

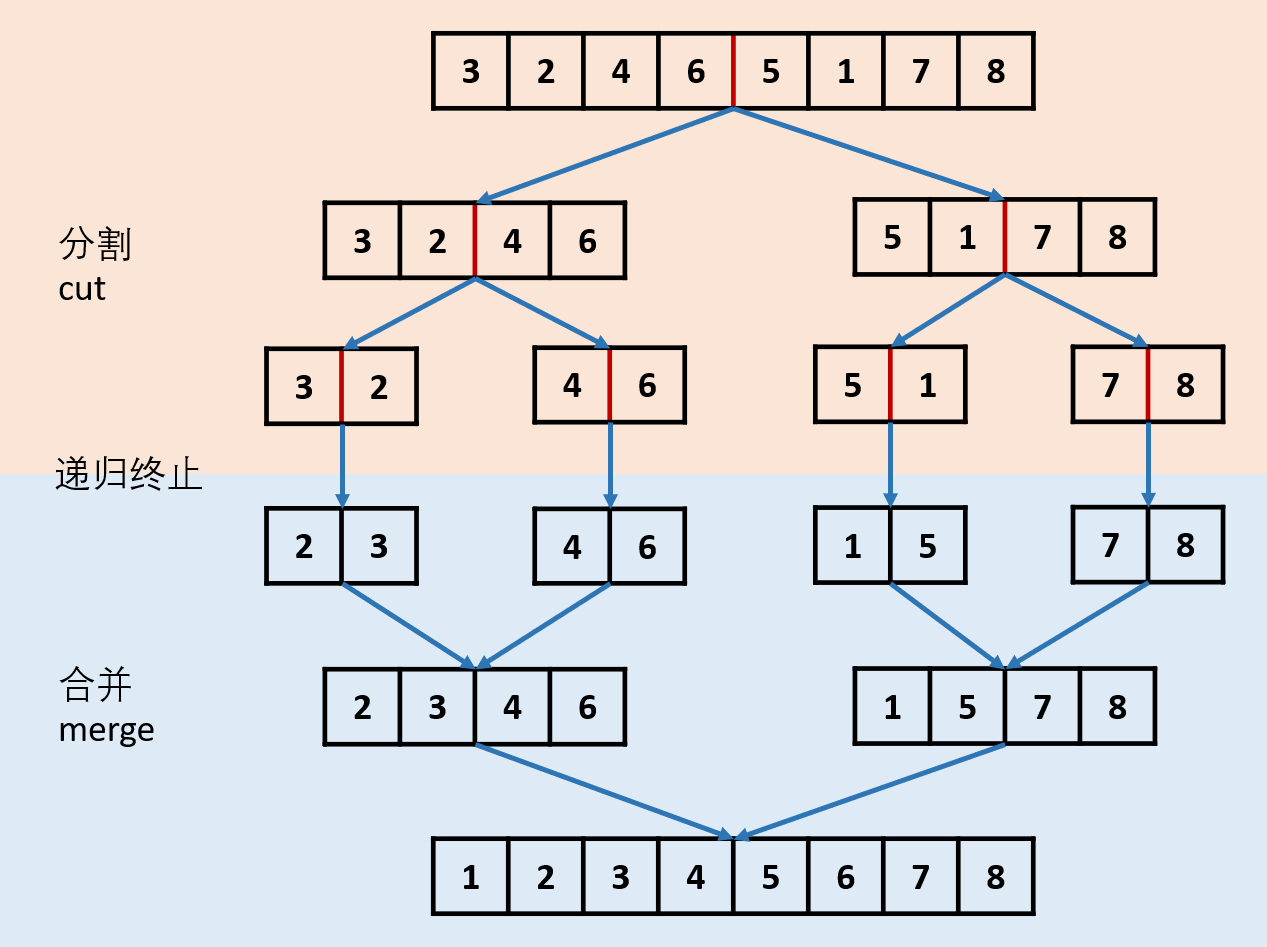
分割 cut 环节：

• 找到当前链表 中点，并从 中点 将链表断开（以便在下次递归 cut 时，链表片段拥有正确边界）；
• 我们使用 fast,slow 快慢双指针法，奇数个节点找到中点，偶数个节点找到中心左边的节点。
• 找到中点 slow 后，执行 slow.next = None 将链表切断。
• 递归分割时，输入当前链表左端点 head 和中心节点 slow 的下一个节点 tmp(因为链表是从 slow 切断的)。
• cut 递归终止条件： 当 head.next == None 时，说明只有一个节点了，直接返回此节点。

合并 merge 环节： 将两个排序链表合并，转化为一个排序链表。

• 双指针法合并，建立辅助 ListNode h 作为头部。
• 设置两指针 left, right 分别指向两链表头部，比较两指针处节点值大小，由小到大加入合并链表头部，指针交替前进，直至添加完两个链表。
• 返回辅助ListNode h 作为头部的下个节点 h.next。
• 时间复杂度 O(l + r)，l, r 分别代表两个链表长度。

当题目输入的 head == None 时，直接返回 None。

代码

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
    public ListNode sortList(ListNode head) {
        // 1. 递归出口
        if (head == null || head.next == null) return head;

        // 2. 快慢指针找中点，把链表切成两段
        ListNode fast = head.next, slow = head;
        while (fast != null && fast.next != null) {
            slow = slow.next;
            fast = fast.next.next;
        }
        ListNode mid = slow.next;
        slow.next = null;                   // 断链

        // 3. 递归排序左右两段
        ListNode left = sortList(head);
        ListNode right = sortList(mid);

        // 4. 合并已排序链表
        ListNode dummy = new ListNode(0);
        ListNode curr = dummy;
        while (left != null && right != null) {
            if (left.val < right.val) {
                curr.next = left;
                left = left.next;
            } else {
                curr.next = right;
                right = right.next;
            }
            curr = curr.next;
        }
        curr.next = left != null ? left : right;
        return dummy.next;
    }
}

复杂度

维度	结论	说明
时间复杂度	O(n log n)	归并排序分解 + 合并
空间复杂度	O(log n)	递归栈深度，n 为链表长度

易错点

易错点	正确姿势
快慢指针写错导致切链不均	fast 初始设为 head.next，slow 停在左段末尾
合并时忘记断链	先 slow.next = null 再递归
合并后未正确接剩余段	合并循环后直接把剩余链表挂到 curr.next
空间要求 O(1) 场景	面试可追问 自底向上归并（迭代版） 实现

23《合并 K 个升序链表》

思路

• 最小堆（优先队列） 多路归并：
  1. 把所有链表的 非空头节点 加入小根堆，按节点值排序。
  2. 每次弹出堆顶最小节点，接到结果链表末尾。
  3. 若该节点还有后续节点，将其后续节点继续入堆。
• 时间复杂度 **O(L log m)**，L 为所有链表节点总数，m 为链表条数。
• 空间复杂度 **O(m)**，堆中同时最多存放 m 个节点。

代码

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
    public ListNode mergeKLists(ListNode[] lists) {
        // 最小堆：按节点值升序
        PriorityQueue<ListNode> queue = new PriorityQueue<>((a, b) -> a.val - b.val);

        // 1. 入堆：每链表的首节点
        for (ListNode list : lists) {
            if (list != null) queue.offer(list);
        }

        ListNode dummy = new ListNode();
        ListNode cur = dummy;

        // 2. 出堆 & 接链
        while (!queue.isEmpty()) {
            ListNode tmp = queue.poll();    // 当前最小节点
            cur.next = tmp;                 // 接在结果链表
            cur = cur.next;

            // 3. 如果该节点还有后续节点，继续入堆
            if (tmp.next != null) queue.offer(tmp.next);
        }

        return dummy.next;
    }
}

复杂度

维度	结论	说明
时间复杂度	O(L log m)	L 为所有链表节点总数，m 为链表条数
空间复杂度	O(m)	堆中最多同时存放 m 个节点

易错点

易错点	正确姿势
忘记判空链表	入堆前检查 list != null
使用 == 比较节点值	优先队列自定义比较器用 a.val - b.val
未将后续节点继续入堆	出堆后判断 tmp.next != null 再 offer
堆容量设置过大	默认 PriorityQueue 即可，无需显式容量
返回原头结点而非 dummy.next	始终返回 dummy.next 保证结果正确

146《LRU缓存机制》

思路

• 数据结构：哈希表 + 双向链表
  • HashMap<Integer, Node> 实现 key → 节点 的 O(1) 查找
  • 双向链表（带哨兵 dummy）按 访问时间升序 维护节点，头为最新，尾为最旧
• 操作规则
  • get：查到节点后，先移除再插入头部（变最新）
  • put：
    1. key 已存在 → 更新值并移到头部
    2. key 不存在 → 新建节点插头部，若超容量则移除尾部节点
• 所有操作 O(1) 时间复杂度

代码

class LRUCache {
    class Node {
        int key, val;
        Node pre, next;
        Node(int k, int v) { key = k; val = v; }
    }

    private final int capacity;
    private final Map<Integer, Node> keyToNode = new HashMap<>();
    private final Node dummy = new Node(-1, -1);

    public LRUCache(int capacity) {
        this.capacity = capacity;
        dummy.next = dummy;
        dummy.pre = dummy;
    }

    public int get(int key) {
        Node node = getNode(key);
        return node == null ? -1 : node.val;
    }

    public void put(int key, int value) {
        Node node = getNode(key);
        if (node != null) {          // 已存在：更新值并置最新
            node.val = value;
            return;
        }

        Node newNode = new Node(key, value);
        addFirst(newNode);
        keyToNode.put(key, newNode);

        if (keyToNode.size() > capacity) { // 超容量：删尾部
            Node tail = dummy.pre;
            remove(tail);
            keyToNode.remove(tail.key);
        }
    }

    /* 把节点挪到头部（最新） */
    private Node getNode(int key) {
        if (!keyToNode.containsKey(key)) return null;
        Node node = keyToNode.get(key);
        remove(node);
        addFirst(node);
        return node;
    }

    /* 链表头插 */
    private void addFirst(Node x) {
        x.next = dummy.next;
        x.pre = dummy;
        dummy.next.pre = x;
        dummy.next = x;
    }

    /* 链表删除 */
    private void remove(Node x) {
        x.pre.next = x.next;
        x.next.pre = x.pre;
    }
}

复杂度

维度	结论	说明
时间复杂度	O(1)	所有操作均为常数时间
空间复杂度	O(capacity)	哈希表 + 双向链表实际节点数

易错点

易错点	正确姿势
未使用哨兵 dummy	用 dummy 头尾指针避免空指针
节点移动未拆链再插	先 remove 再 addFirst 保证顺序
容量判断位置错误	插入新节点后再判断并删除最旧节点
删除尾部时忘记清哈希表	同时 remove 链表节点 + keyToNode.remove

TODO LFU

二叉树

94《二叉树的中序遍历》

思路

按照 左子树 → 根节点 → 右子树 的顺序递归访问整棵树，并收集节点值。

• 数据结构：二叉树
• 遍历方式：深度优先搜索（DFS）——中序递归
• 实现要点
  1. 递归终止条件：root == null。
  2. 先递归左子树，再访问根节点，最后递归右子树。
• 每个节点仅访问一次，时间复杂度 **O(n)**，空间复杂度 **O(h)**（递归栈深度，h 为树高）。

代码

class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> res = new ArrayList<>();
        inorder(root, res);
        return res;
    }

    // 辅助递归函数：中序遍历以 root 为根的子树，并把结果加入 res
    private void inorder(TreeNode root, List<Integer> res) {
        if (root == null) return;

        inorder(root.left, res);   // 左
        res.add(root.val);         // 根
        inorder(root.right, res);  // 右
    }
}

复杂度

维度	结论	说明
时间复杂度	O(n)	每个节点仅被访问一次
空间复杂度	O(h)	递归栈深度，最坏链表高度 n

易错点

易错点	正确姿势
递归顺序写错	严格按照 左 → 根 → 右 的顺序
未判空直接递归	先检查 root == null 再递归

104《二叉树的最大深度》

思路

递归地计算左右子树的最大深度，当前节点深度 = max(左深度, 右深度) + 1。

• 数据结构：二叉树

• 遍历方式：深度优先搜索（DFS）后序遍历

• 递归公式

  maxDepth(root) = max(maxDepth(root.left), maxDepth(root.right)) + 1
  

• 每个节点仅访问一次，时间复杂度 **O(n)**，空间复杂度 **O(h)**（递归栈深度，h 为树高）。

---

代码

class Solution {
    public int maxDepth(TreeNode root) {
        return computeDepth(root);
    }

    // 辅助函数：返回以 root 为根的子树的最大深度
    private int computeDepth(TreeNode root) {
        if (root == null) return 0;

        int leftDepth  = computeDepth(root.left);
        int rightDepth = computeDepth(root.right);

        return Math.max(leftDepth, rightDepth) + 1;
    }
}

---

复杂度

维度	结论	说明
时间复杂度	O(n)	每个节点仅访问一次
空间复杂度	O(h)	递归栈深度，最坏链表高度 n

---

易错点

易错点	正确姿势
未处理空树	空节点返回 0
忘记加 1	当前节点自身深度需 +1
辅助函数暴露为 public	递归辅助函数建议用 private，保持接口简洁

543《二叉树直径》

思路

直径定义为 任意两节点间最长路径的边数（注意题目要求的是 边数，而不是节点数）。
最长路径一定经过某个节点的 左高 + 右高，因此可在一次 后序遍历 中同时：

1. 计算当前节点的高度（到叶子节点的边数）。
2. 用 左高 + 右高 更新全局最大直径。

• 遍历方式：后序 DFS（自底向上）
• 关键点
  • 全局变量 maxD 保存当前最大直径。
  • 每个节点返回自身高度，供父节点拼接。
• 每个节点仅访问一次，时间复杂度 **O(n)**，空间复杂度 **O(h)**（递归栈深度）。

---

代码

class Solution {
    private int maxD = 0;          // 全局最大直径（边数）

    public int diameterOfBinaryTree(TreeNode root) {
        height(root);
        return maxD;
    }

    // 返回以 root 为根的子树高度（到叶子节点的边数）
    private int height(TreeNode root) {
        if (root == null) return 0;          // 空子树高度为 0

        int leftH  = height(root.left);      // 左子树高度
        int rightH = height(root.right);     // 右子树高度

        maxD = Math.max(maxD, leftH + rightH); // 经过当前节点的直径

        return Math.max(leftH, rightH) + 1;  // 当前高度
    }
}

---

复杂度

维度	结论	说明
时间复杂度	O(n)	每个节点仅访问一次
空间复杂度	O(h)	递归栈深度，最坏链表高度 n

---

易错点

易错点	正确姿势
把直径当成节点数	题目要求的是 边数，所以 leftH + rightH 即可
只递归未更新全局变量	必须维护 maxD，并在后序时实时更新
返回高度时忘记 +1	当前节点到子节点有一条边，高度为 max(leftH, rightH) + 1

226《翻转二叉树》

思路

前序遍历（根 → 左 → 右） 的递归框架：
先处理当前节点（交换左右孩子），再递归处理左右子树。

• 遍历方式：前序 DFS
  1. 访问根节点：交换 left 与 right。
  2. 递归翻转左子树。
  3. 递归翻转右子树。
• 每个节点仅访问一次，时间复杂度 **O(n)**，空间复杂度 **O(h)**。

---

代码

class Solution {
    public TreeNode invertTree(TreeNode root) {
        if (root == null) return null;

        // 1. 根：交换左右子树
        TreeNode tmp = root.left;
        root.left = root.right;
        root.right = tmp;

        // 2. 左：递归翻转左子树
        invertTree(root.left);
        // 3. 右：递归翻转右子树
        invertTree(root.right);

        return root;
    }
}

---

复杂度

维度	结论	说明
时间复杂度	O(n)	每个节点仅访问一次
空间复杂度	O(h)	递归栈深度，最坏链表高度 n

---

易错点

易错点	正确姿势
交换后忘记递归	交换完仍需递归处理左右子树
新建节点浪费内存	仅交换指针，不创建新节点

101《对称二叉树》

思路

将“对称”判定问题转化为 两棵子树互为镜像 的问题。
采用 深度优先搜索（DFS）前序遍历 同时遍历两棵子树，一树向左、一树向右，边遍历边比较。

• 遍历方式：双指针 DFS
  1. 比较当前节点值。
  2. 递归比较外侧：左左 vs 右右。
  3. 递归比较内侧：左右 vs 右左。
• 每个节点仅访问一次，时间复杂度 **O(n)**，空间复杂度 **O(h)**（递归栈深度）。

---

代码

class Solution {
    public boolean isSymmetric(TreeNode root) {
        if (root == null) return true;          // 空树视为对称
        return compare(root.left, root.right);  // 从左右子树开始比较
    }

    // 判断两棵子树是否互为镜像
    private boolean compare(TreeNode left, TreeNode right) {
        // 1. 同时为空 → 对称
        if (left == null && right == null) return true;
        // 2. 仅一个为空 → 不对称
        if (left == null || right == null) return false;
        // 3. 值不相等 → 不对称
        if (left.val != right.val) return false;

        // 4. 递归比较外侧与内侧
        boolean outer = compare(left.left, right.right);
        boolean inner = compare(left.right, right.left);
        return outer && inner;
    }
}

---

复杂度

维度	结论	说明
时间复杂度	O(n)	每个节点仅访问一次
空间复杂度	O(h)	递归栈深度，最坏链表高度 n

---

易错点

易错点	正确姿势
未区分外侧、内侧递归	明确 left.left vs right.right 与 left.right vs right.left
使用按位与 & 替代逻辑与 &&	返回布尔值应使用 &&，语义更清晰
未处理空树	空树直接返回 true，视为对称

437《路径总和 III》

思路

双层递归，枚举每个节点作为路径起点，向下累加节点值，实时减目标值，统计满足条件的路径。

• 枚举策略
  1. 把每个节点都当成一次新的起点。
  2. 从该起点向下深度优先累加节点值，实时用剩余目标值 target - node.val 判断是否凑够。
• 双递归框架
  • pathSum：外层递归，枚举整棵树的所有节点为起点。
  • dfs：内层递归，从给定节点出发向下统计满足条件的路径数。
• 所有节点都会被枚举一次，每棵子树也会被完整遍历一次，时间复杂度 **O(n²)**，空间复杂度 **O(n)**（递归栈）。

代码

class Solution {
    public int pathSum(TreeNode root, int targetSum) {
        if (root == null) return 0;               // 空树直接返回 0
        int rootSum = dfs(root, targetSum);       // ① 以当前节点为起点
        int leftSum = pathSum(root.left, targetSum);  // ② 枚举左子树所有起点
        int rightSum = pathSum(root.right, targetSum); // ③ 枚举右子树所有起点
        return rootSum + leftSum + rightSum;      // 汇总整棵树结果
    }
    
    private int dfs(TreeNode node, long target) {
        if (node == null) return 0;
        int count = 0;                            // 必须放在函数内，防止跨路径污染
        if (node.val == target) count++;          // 当前节点恰好满足
        count += dfs(node.left,  target - node.val);  // 左分支继续找剩余和
        count += dfs(node.right, target - node.val);  // 右分支继续找剩余和
        return count;                             // 返回以 node 为起点的总条数
    }
}

复杂度

维度	结论	说明
时间复杂度	O(n²)	最坏情况下退化成链表，每个节点都向下遍历
空间复杂度	O(n)	递归栈深度，最坏链表高度 n

易错点

易错点	正确姿势
把 count 写成全局变量	必须放在 dfs 函数内部，避免不同起点结果相互污染
漏掉左右子树继续枚举起点	外层递归一定要 pathSum(root.left/right) 而非 dfs
未用 long 存 target	节点值可能很大，累减后可能溢出 int

124《二叉树中的最大路径和》

思路

• 数据结构：二叉树
• 遍历方式：一次 后序遍历（DFS 自底向上）
• 核心思想
  1. 每个节点视为路径的 “最高点”。
  2. 计算两条值：
     • 单边最大贡献：只能选左或右一条分支继续向上延伸（负值直接舍弃为 0）。
     • 完整路径和：左 + 根 + 右 三者之和，用于更新全局最大值。
  3. 全局变量 maxSum 实时记录 最大路径和。
• 所有节点仅访问一次，时间复杂度 **O(n)**，空间复杂度 **O(h)**（树高）。

代码

class Solution {
    int maxSum = Integer.MIN_VALUE;   // 全局最大路径和

    public int maxPathSum(TreeNode root) {
        dfs(root);                    // 启动后序遍历
        return maxSum;
    }

    /**
     * 后序遍历：返回以当前节点为根的“单边最大贡献”
     * @param root 当前节点
     * @return 当前节点能给父节点提供的最大单边和（≥0）
     */
    private int dfs(TreeNode root) {
        if (root == null) return 0;

        // 左右子树的单边最大贡献（负数直接取 0 表示不选）
        int leftGain  = Math.max(dfs(root.left),  0);
        int rightGain = Math.max(dfs(root.right), 0);

        // 以当前节点为“最高点”的完整路径和
        int curPathSum = root.val + leftGain + rightGain;
        maxSum = Math.max(maxSum, curPathSum);    // 更新全局最大

        // 返回给父节点的单边贡献：只能选较大的一边 + 当前节点值
        return root.val + Math.max(leftGain, rightGain);
    }
}

复杂度

维度	结论	说明
时间复杂度	O(n)	每个节点仅访问一次
空间复杂度	O(h)	递归栈深度，h 为树高

易错点

易错点	正确姿势
未用全局变量记录最大值	维护 maxSum 并在后序过程中实时更新
负增益未舍弃	Math.max(dfs(...), 0) 忽略负值贡献
返回值写成完整路径和	返回的是 单边贡献，只能选左或右 + 当前节点
初始 maxSum 设为 0	应设为 Integer.MIN_VALUE 防止全负数树出错

与 437 题思想对比

维度	437 题（路径总和 III）	124 题（最大路径和）
起点	枚举 所有节点 作为起点	每个节点只做 一次后序计算
递归层数	双层递归，O(n²)	单层后序，O(n)
返回值	路径条数	单边最大贡献（给父节点用）
全局变量	无	记录全局最大路径和

236《二叉树的最近公共祖先》

思路

• 数据结构：普通二叉树（BST 性质未知）
• 遍历方式：一次 后序遍历（DFS 自底向上）
• 核心思想
  1. 若当前节点为 null 或等于 p / q，直接返回该节点。
  2. 递归左右子树，得到左右搜索结果 left、right。
  3. 根据搜索结果判断：
     • left 与 right 均非空 → 当前节点即为 LCA。
     • 仅一侧非空 → 非空侧继续向上传递。
     • 均空 → 返回 null。
• 每个节点仅访问一次，时间复杂度 **O(n)**，空间复杂度 **O(h)**（树高）。

图片来自：二叉树的最近公共祖先【基础算法精讲 12】_哔哩哔哩_bilibili

代码

class Solution {
    /**
     * 后序遍历：自底向上寻找最近公共祖先
     * @param root 当前子树根节点
     * @param p    目标节点1
     * @param q    目标节点2
     * @return     LCA 节点或 null
     */
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        // 1. 命中空节点或找到 p/q 直接返回
        if (root == null || root == p || root == q) return root;

        // 2. 后序遍历左右子树
        TreeNode left  = lowestCommonAncestor(root.left,  p, q);
        TreeNode right = lowestCommonAncestor(root.right, p, q);

        // 3. 根据左右结果判断
        if (left != null && right != null) return root; // 左右均找到，当前即 LCA
        return left != null ? left : right;             // 仅一侧非空，继续向上
        //只要 left 非空，就返回 left；否则返回 right（此时如果 right 也是 null，自然返回 null）。
        //和下面的等价
        //if (left != null) return left;
        //if (right != null) return right;
        //return null;
    }
}

复杂度

维度	结论	说明
时间复杂度	O(n)	每个节点仅访问一次
空间复杂度	O(h)	递归栈深度，h 为树高

易错点

易错点	正确姿势
未判断当前节点等于 p/q 的情况	直接返回当前节点，作为向上传递的“信号”
递归后未正确处理左右结果合并	左右均非空才说明当前节点是 LCA
递归前提前剪枝导致漏解	必须完整遍历整棵树，不能提前返回

108《将有序数组转换为二叉搜索树》

思路

给定升序数组，要求构造高度平衡的二叉搜索树（BST）。
核心：每次取区间中点作为根节点，保证左右子树节点数相差 ≤ 1。

• 数据结构：升序数组 + 二叉搜索树
• 遍历方式：递归（分治）
• 关键步骤
  1. 取当前区间 [l, r] 的中点 mid 作为根节点。
  2. 递归构建左子树 [l, mid-1]。
  3. 递归构建右子树 [mid+1, r]。
• 每个元素仅访问一次，时间复杂度 **O(n)**，空间复杂度 **O(log n)**（递归栈高度）。

---

代码

class Solution {
    public TreeNode sortedArrayToBST(int[] nums) {
        return build(nums, 0, nums.length - 1);
    }

    // 辅助函数：将 nums[l..r] 构造成平衡 BST
    private TreeNode build(int[] nums, int l, int r) {
        if (l > r) return null;

        int mid = (l + r) >>> 1;          // 防溢出位运算
        TreeNode root = new TreeNode(nums[mid]);

        root.left = build(nums, l, mid - 1);
        root.right = build(nums, mid + 1, r);

        return root;
    }
}

---

复杂度

维度	结论	说明
时间复杂度	O(n)	每个元素仅访问一次
空间复杂度	O(log n)	递归栈深度，最坏为完全平衡树高度 log₂n

---

易错点

易错点	正确姿势
中点计算溢出	使用 (l + r) >>> 1 或 l + (r - l) / 2
区间边界错误	左子树 [l, mid-1]，右子树 [mid+1, r]
递归终止条件写成 l >= r	应为 l > r，区间为空时才返回 null

98《验证二叉搜索树》

思路

利用 BST 的上下界递归验证 思想：
每个节点在递归过程中都被赋予一个 **允许区间 (lower, upper)**，只有当其值落在此区间时才继续递归左右子树，并进一步收紧边界。

• 左子树所有节点值必须 < 当前节点值 → 新区间 (lower, root.val)
• 右子树所有节点值必须 > 当前节点值 → 新区间 (root.val, upper)

• 遍历方式：先序 DFS（根 → 左 → 右）
• 时间复杂度 **O(n)**，空间复杂度 **O(h)**（递归栈深度，h 为树高）。

---

代码

class Solution {
    public boolean isValidBST(TreeNode root) {
        return isValid(root, Long.MIN_VALUE, Long.MAX_VALUE);
    }

    // 验证以 root 为根的子树所有节点值都在 (lower, upper) 内
    private boolean isValid(TreeNode root, long lower, long upper) {
        if (root == null) return true;

        // 当前节点值必须严格在区间内
        if (root.val <= lower || root.val >= upper) return false;

        // 递归验证左右子树，并收紧边界
        return isValid(root.left,  lower, root.val)
            && isValid(root.right, root.val, upper);
    }
}

---

复杂度

维度	结论	说明
时间复杂度	O(n)	每个节点仅访问一次
空间复杂度	O(h)	递归栈深度，最坏链表高度 n

---

易错点

易错点	正确姿势
使用 int 边界导致溢出	采用 long 作为上下界初始值 (MIN/MAX_VALUE)
允许等于边界	必须 严格小于/大于，即 < 与 >
递归时边界传递错误	左子树更新 upper = root.val，右子树更新 lower = root.val
遍历顺序未说明	明确采用 先序 DFS，根节点先验证再递归

105《从前序与中序遍历序列构造二叉树》

思路

• 数据结构：二叉树
• 遍历方式：分治递归
• 核心思想
  1. 前序遍历第 1 个元素即为 根节点。
  2. 在中序遍历中找到该根节点，其左侧为 左子树中序区间，右侧为 右子树中序区间。
  3. 根据左子树长度，切分出 左/右子树的前序区间，递归构造左右子树。
• 每次递归区间长度减 1，时间复杂度 **O(n²)**（copyOfRange 每次 O(n)），空间复杂度 **O(n)**（递归栈 + 新数组）。
  若改用索引传递，可将时间优化到 **O(n)**。

代码

class Solution {
    public TreeNode buildTree(int[] preorder, int[] inorder) {
        int m = preorder.length;
        int n = inorder.length;
        if (m == 0 || n == 0) return null;

        // 1. 前序首元素为根
        TreeNode root = new TreeNode(preorder[0]);

        // 2. 在中序中找到根的位置 i
        for (int i = 0; i < n; i++) {
            if (preorder[0] == inorder[i]) {
                // 3. 切分中序：左 [0, i)   右 (i, end)
                int[] inLeft  = Arrays.copyOfRange(inorder, 0, i);
                int[] inRight = Arrays.copyOfRange(inorder, i + 1, n);

                // 4. 切分前序：左 [1, 1+i) 右 [1+i, end)
                int[] preLeft  = Arrays.copyOfRange(preorder, 1, 1 + i);
                int[] preRight = Arrays.copyOfRange(preorder, 1 + i, m);

                // 5. 递归构造左右子树
                root.left  = buildTree(preLeft, inLeft);
                root.right = buildTree(preRight, inRight);
                break;
            }
        }
        return root;
    }
}

复杂度

维度	结论	说明
时间复杂度	O(n²)	每次 copyOfRange 需 O(n)，共 n 次
空间复杂度	O(n)	递归栈 + 新数组

易错点

易错点	正确姿势
数组边界写错	copyOfRange 右端开区间，注意长度一致
前序/中序索引混淆	前序区间 起始下标为 1（根占 0），中序区间 起始下标为 0
忘记处理空数组	入口先判空直接返回 null
前序区间起点/长度计算错误	左子树长度 = 中序左区间长度

114《二叉树展开为链表》

思路

• 数据结构：二叉树
• 遍历方式：先序遍历（Pre-order）
• 核心思想
  1. 先序遍历整棵树，把节点按访问顺序保存到列表。
  2. 遍历列表，依次把每个节点的 left 置 null，right 指向下一节点，形成单链表。
• 时间复杂度 **O(n)**，空间复杂度 **O(n)**（递归栈 + 列表）。
  可优化为 O(1) 空间的“原地展开”：边遍历边修改指针。

代码

class Solution {
    private final List<TreeNode> res = new ArrayList<>();

    public void flatten(TreeNode root) {
        if (root == null) return;

        preOrder(root);                      // 1. 先序遍历收集节点

        // 2. 按顺序重接指针
        for (int i = 0; i < res.size() - 1; i++) {
            TreeNode cur = res.get(i);
            cur.left  = null;                // 左指针置空
            cur.right = res.get(i + 1);      // 右指针指向下一个节点
        }
    }

    /** 先序遍历：根 → 左 → 右 */
    private void preOrder(TreeNode root) {
        if (root == null) return;
        res.add(root);         // 根
        preOrder(root.left);   // 左
        preOrder(root.right);  // 右
    }
}

复杂度

维度	结论	说明
时间复杂度	O(n)	每个节点被访问一次
空间复杂度	O(n)	递归栈 + res 列表

易错点

易错点	正确姿势
未清空 left 指针	必须显式 cur.left = null，否则会形成环
数组越界	循环范围 i < res.size() - 1，留最后一个节点
空树未提前返回	入口 if (root == null) return
原地展开时破坏遍历结构	若用原地法，需“右-左-根”逆序遍历或 Morris 遍历

有！除了“先序遍历 + 列表”的做法，114 题还有 两种常见 O(1) 额外空间 的原地解法，下面给出思路、代码与对比。

---

解法 2：迭代 + 前驱指针（O(1) 空间）

思路

1. 从根开始迭代。
2. 对于每个节点：
   • 如果 左子树为空，直接往右走一步。
   • 如果 左子树非空：
     • 找到左子树 最右节点（前驱）。
     • 把 当前右子树 接到前驱的右指针。
     • 把 左子树整体移到右边，并置空左指针。
3. 重复直到整棵树变成链表。

代码

class Solution {
    public void flatten(TreeNode root) {
        TreeNode cur = root;
        while (cur != null) {
            if (cur.left != null) {              // 有左子树
                TreeNode pre = cur.left;         // 找前驱
                while (pre.right != null) pre = pre.right;
                pre.right = cur.right;           // 右子树挂到前驱
                cur.right = cur.left;            // 左子树移到右边
                cur.left = null;                 // 置空左指针
            }
            cur = cur.right;                     // 继续处理下一个节点
        }
    }
}

解法 3：后序遍历 + 指针反转（O(1) 空间，面试高频）

思路

• 采用 逆序后序遍历（右 → 左 → 根）。
• 维护一个 prev 指针：始终指向 已展开的链表头。
• 每访问一个节点：
  • 把 left 置空，把 right 指向 prev，
  • 更新 prev = 当前节点，继续向上。

代码

class Solution {
    private TreeNode prev = null;

    public void flatten(TreeNode root) {
        if (root == null) return;
        flatten(root.right);  // 先右
        flatten(root.left);   // 再左
        root.left = null;     // 置空左
        root.right = prev;    // 接链表头
        prev = root;          // 更新链表头
    }
}

---

三种做法对比

方案	时间	额外空间	核心技巧	代码简洁度
先序+列表	O(n)	O(n)	遍历后顺序重接指针	★★★☆☆
迭代前驱	O(n)	O(1)	找前驱，原地搬子树	★★★★☆
后序指针	O(n)	O(1)	逆序后序，prev 倒插	★★★★☆

102《二叉树的层序遍历》

思路

广度优先搜索（BFS）逐层展开，用队列保存当前层的所有节点，循环处理。

• 数据结构：二叉树
• 遍历方式：BFS（队列）
• 核心步骤
  1. 先把根节点入队。
  2. 每次循环开始时记录当前队列长度 len，即当前层的节点个数。
  3. 依次弹出 len 个节点，收集它们的值，并将左右孩子入队，形成下一层。
• 每个节点仅入队、出队各一次，时间复杂度 **O(n)**，空间复杂度 **O(n)**（队列最坏宽度）。

代码

class Solution {
    public List<List<Integer>> levelOrder(TreeNode root) {
        List<List<Integer>> res = new ArrayList<>();
        if (root == null) return res;

        Queue<TreeNode> queue = new LinkedList<>();
        queue.offer(root);

        while (!queue.isEmpty()) {
            int len = queue.size();            // 当前层节点数
            List<Integer> levelRes = new ArrayList<>();
            while (len-- > 0) {                // 处理整层
                TreeNode node = queue.poll();
                levelRes.add(node.val);        // 收集值
                if (node.left != null) queue.offer(node.left);
                if (node.right != null) queue.offer(node.right);
            }
            res.add(levelRes);                 // 当前层结果加入总答案
        }
        return res;
    }
}

复杂度

维度	结论	说明
时间复杂度	O(n)	每个节点仅进出队列一次
空间复杂度	O(n)	队列最大宽度，最坏情况为满二叉树

易错点

易错点	正确姿势
用 pull() 代替 poll()	队列接口只有 poll() / remove() / offer() 等方法
把节点值直接加到结果列表	应先收集到 levelRes，再把整层列表加入 res
循环内未记录当前层节点个数	必须在进入内层循环前用 len = queue.size() 固定长度

199《二叉树的右视图》

思路

层序遍历（BFS）的“最后一节点”视角：每层只保留 最右侧节点值。

• 数据结构：二叉树
• 遍历方式：BFS（队列）
• 核心步骤
  1. 正常层序遍历。
  2. 每层循环中，当 len == 1 时把当前节点值加入结果即可。
• 时间复杂度 **O(n)**，空间复杂度 **O(n)**。

代码

class Solution {
    public List<Integer> rightSideView(TreeNode root) {
        List<Integer> ans = new ArrayList<>();
        if (root == null) return ans;

        Queue<TreeNode> queue = new LinkedList<>();
        queue.offer(root);

        while (!queue.isEmpty()) {
            int len = queue.size();
            for (int i = 0; i < len; i++) {
                TreeNode node = queue.poll();
                if (i == len - 1) ans.add(node.val); // 每层最后一个节点
                if (node.left != null) queue.offer(node.left);
                if (node.right != null) queue.offer(node.right);
            }
        }
        return ans;
    }
}

复杂度

维度	结论	说明
时间复杂度	O(n)	每个节点仅访问一次
空间复杂度	O(n)	队列宽度，最坏满二叉树

易错点

易错点	正确姿势
返回 List<List<Integer>>	方法签名要求返回 List<Integer>
用 levelRes 再包一层	直接收集每层最后一个节点值即可
忘记判断 root == null	空树直接返回空列表

199-扩展《二叉树的左视图》

思路

同样利用 层序遍历（BFS），但每层只取 最左侧节点值。

• 数据结构：二叉树
• 遍历方式：BFS（队列）
• 关键改动
  1. 正常层序遍历。
  2. 每层循环中，当 i == 0 时把当前节点值加入结果即可。
• 时间复杂度 **O(n)**，空间复杂度 **O(n)**。

代码

class Solution {
    public List<Integer> leftSideView(TreeNode root) {
        List<Integer> ans = new ArrayList<>();
        if (root == null) return ans;

        Queue<TreeNode> queue = new LinkedList<>();
        queue.offer(root);

        while (!queue.isEmpty()) {
            int len = queue.size();
            for (int i = 0; i < len; i++) {
                TreeNode node = queue.poll();
                if (i == 0) ans.add(node.val);   // 每层第一个节点
                if (node.left != null) queue.offer(node.left);
                if (node.right != null) queue.offer(node.right);
            }
        }
        return ans;
    }
}

复杂度

维度	结论	说明
时间复杂度	O(n)	每个节点仅访问一次
空间复杂度	O(n)	队列宽度，最坏满二叉树

易错点

易错点	正确姿势
仍然取 i == len - 1	应改为 i == 0 获取最左侧节点
忘记处理空树	root == null 时直接返回空列表
返回 List<List<Integer>>	方法签名要求返回 List<Integer>

TODO 二叉树的俯视图

哈希

1《两数之和》

思路

一次遍历 + 哈希表 实现 O(n) 查询：
在遍历 nums 的同时，把已访问过的元素及其下标存入 HashMap；
对于当前元素 nums[i]，只需在表中查找是否存在 target - nums[i]。

• 若存在 → 直接返回结果；
• 若不存在 → 把 nums[i] 及下标 i 存入表中，继续。

• 数据结构：HashMap<值, 下标>
• 遍历方式：一次顺序遍历（前向扫描）
• 时间复杂度 **O(n)**，空间复杂度 **O(n)**。

---

代码

class Solution {
    public int[] twoSum(int[] nums, int target) {
        HashMap<Integer,Integer> map = new HashMap<>();
        int[] res = new int[2];
        for(int i=0;i<nums.length;i++){
            int tmp = target-nums[i];
            if(map.containsKey(tmp)) {
                res[0]=map.get(tmp);
                res[1]=i;
                return res;
            }

            map.put(nums[i],i);
        }
        return res;
    }
}

---

复杂度

维度	结论	说明
时间复杂度	O(n)	每个元素最多被哈希表查询一次
空间复杂度	O(n)	哈希表最多存储 n 个元素

---

易错点

易错点	正确姿势（避坑指南）
忘记 containsKey/get 用法	先 containsKey(key) 判断，再 get(key) 取索引
先 put 再查询	必须先查询，再 put，否则会把同一下标重复计入
未立即返回结果	一旦找到匹配对，立即 return new int[]{...}，避免多余循环

49《字母异位词分组》

思路

利用排序后的字符串作为异位词的唯一标识；
按标识分组，最终把哈希表的所有值收集成列表返回。

• 数据结构：Map<String, List<String>>
• 遍历方式：一次顺序遍历
• 时间复杂度 **O(n · k log k)**，空间复杂度 **O(n · k)**。

---

代码（保留原实现，仅加注释）

class Solution {
    public List<List<String>> groupAnagrams(String[] strs) {
        // key：排序后的字符串；value：属于同一组的原始字符串列表
        Map<String, List<String>> map = new HashMap<>();

        for (String str : strs) {
            // 1. 生成特征 key：把原字符串排序
            char[] ch = str.toCharArray();
            Arrays.sort(ch);
            String sortedStr = new String(ch);

            // 2. 如果 map 中没有该 key，先放一个空列表占位
            if (!map.containsKey(sortedStr)) {
                map.put(sortedStr, new ArrayList<>());
            }

            // 3. 将当前字符串加入对应的分组
            map.get(sortedStr).add(str);
        }

        // 4. 把哈希表里所有分组一次性转成 List<List<String>>
        return new ArrayList<>(map.values());
    }
}

---

复杂度

维度	结论	说明
时间复杂度	O(n · k log k)	每个字符串排序耗时 k log k
空间复杂度	O(n · k)	哈希表存储全部字符串

---

易错点

易错点	正确姿势（已在代码体现）
先查后放，逻辑正确	使用 containsKey + put + get 三连
未排序直接当 key	已用 Arrays.sort 保证 key 一致
返回格式不正确	用 new ArrayList<>(map.values()) 构造返回
先初始化空列表	第一次遇到某个 key 此时 map 里还没有这个 sortedStr，直接 map.get(sortedStr) 会返回 null，再调用 .add(str) 就会抛出 空指针异常。

128《最长连续序列》

思路

哈希集合去重 + 一次线性扫描

1. 将所有数字放入 HashSet 去重。
2. 仅当 num-1 不在集合时，才把 num 视为一段连续序列的起点，向后扩展并统计长度。
3. 全局变量记录最大长度。

• 数据结构：HashSet<Integer>
• 遍历方式：一次顺序遍历集合
• 时间复杂度 **O(n)**，空间复杂度 **O(n)**。

---

代码

class Solution {
    public int longestConsecutive(int[] nums) {
        int maxLen = 0;
        HashSet<Integer> set = new HashSet<>();
        // 1. 去重
        for (int num : nums) {
            set.add(num);
        }

        // 2. 只从序列起点开始向后扩展
        for (int n : set) {
            if (set.contains(n - 1)) continue; // 不是起点则跳过

            int curMax = 1;                    // 当前连续长度
            while (set.contains(n + 1)) {
                n++;                           // 向后扩展
                curMax++;
            }
            maxLen = Math.max(curMax, maxLen); // 更新全局最大
        }
        return maxLen;
    }
}

---

复杂度

维度	结论	说明
时间复杂度	O(n)	每个元素最多被访问两次（放入集合 + 扩展）
空间复杂度	O(n)	HashSet 存储全部元素

---

易错点

易错点	正确姿势
未去重	使用 HashSet 去掉重复数字
不从序列起点开始扩展	先判断 n-1 是否存在，避免重复扫描同一条序列
未使用去重后的set做遍历导致超时	要遍历哈希表而不是原始数组，不然会超时，而哈希表去重了，所以遍历效率会高一些

\

双指针

283《移动零》

思路

• 双指针：
  • fast 负责扫描整个数组。
  • slow 指向下一个应该放非零元素的位置。
• 当 fast 遇到非零元素时，与 slow 交换，并同时把 slow 右移一位。
• 遍历结束后，所有非零元素都被集中到数组前端，后面自然全是零。

代码

class Solution {
    public void moveZeroes(int[] nums) {
        int slow = 0;
        for (int fast = 0; fast < nums.length; fast++) {
            if (nums[fast] != 0) {
                swap(nums, slow, fast);
                slow++;
            }
        }
    }

    private void swap(int[] arr, int i, int j) {
        int tmp = arr[i];
        arr[i] = arr[j];
        arr[j] = tmp;
    }
}

复杂度

时间：每个元素只被访问一次，O(n)。
空间：只用到两个指针，O(1)。

易错点

易错点	正确做法	备注
把 slow++ 写在循环外	当交换完成后立即 slow++	否则会把非零元素覆盖掉
自己实现 swap 时写成值互换	必须交换 下标对应元素，而非值本身	数组传参是值传递，需操作数组
忘记写 swap 方法	提取成私有方法，保持主逻辑清晰	也可在循环内直接交换
用额外数组存储结果	题目要求 原地 修改	不额外使用 O(n) 空间

11《盛最多水的容器》

思路

• 双指针：
  • left 指向数组头，right 指向数组尾。
• 面积公式：area = (right - left) * min(height[left], height[right])。
• 贪心策略：
  • 每次把“短板”向中间移动，才可能找到更大的面积；长板移动只会减小或不变。
• 重复上述步骤直到左右指针相遇，过程中记录最大面积。

代码

class Solution {
    public int maxArea(int[] height) {
        int max = 0;                          // 最大面积
        int left = 0;                         // 左指针
        int right = height.length - 1;        // 右指针

        while (left < right) {
            // 计算当前窗口面积
            int area = (right - left) * Math.min(height[left], height[right]);
            max = Math.max(max, area);

            // 移动短板：才可能得到更大面积
            if (height[left] < height[right]) {
                left++;   // 左边矮，左指针右移
            } else {
                right--;  // 右边矮或等高，右指针左移
            }
        }
        return max;
    }
}

复杂度

时间：O(n)，每个位置最多被访问一次。
空间：O(1)，仅用常数级指针。

易错点

易错点	正确做法	备注
把 <= 写成 < 导致死循环	while (left < right)	相等时仍需比较一次面积
移动指针时只移动高板	必须移动 短板	移高板只会使面积更小或不变
面积计算用 max 而非 min	(right - left) * Math.min(...)	盛水量由短板决定
移动短板的时候判断条件写成了if (left < right)	if (height[left] < height[right])	分清楚含义

15《三数之和》

思路

• 排序：先对数组升序，方便双指针与去重。
• 外层循环：固定一个数 nums[i]，把问题转化为在 [i+1, n-1] 中找两数之和等于 -nums[i]。
• 双指针：l = i+1, r = n-1，根据 nums[l] + nums[r] 与 -nums[i] 的大小关系移动指针。
• 去重：
  • 外层跳过重复的 nums[i]；
  • 每找到一组解后，跳过所有重复的 nums[l] 和 nums[r]。
• 剪枝：若 nums[i] > 0，则后续不可能再凑出 0，直接退出。

代码

class Solution {
    public List<List<Integer>> threeSum(int[] nums) {
        List<List<Integer>> res = new ArrayList<>();
        Arrays.sort(nums);
        int n = nums.length;

        for (int i = 0; i < n - 2; i++) {
            // 1. 外层去重
            if (i > 0 && nums[i] == nums[i - 1]) continue;
            // 2. 剪枝
            if (nums[i] > 0) break;

            int target = -nums[i];
            int l = i + 1, r = n - 1;

            while (l < r) {
                int sum = nums[l] + nums[r];
                if (sum < target) {
                    l++;
                } else if (sum > target) {
                    r--;
                } else {
                    res.add(Arrays.asList(nums[i], nums[l], nums[r]));
                    l++; r--;
                    // 3. 内层去重
                    while (l < r && nums[l] == nums[l - 1]) l++;
                    while (l < r && nums[r] == nums[r + 1]) r--;
                }
            }
        }
        return res;
    }
}

复杂度

时间：排序 O(n log n) + 双指针 O(n²) → 总体 O(n²)。
空间：O(1)（忽略返回值占用的空间）。

易错点

易错点	正确做法	备注
外层未去重	if (i > 0 && nums[i] == nums[i - 1]) continue;	防止重复三元组
未剪枝	if (nums[i] > 0) break;	升序后若最小数>0，后面必>0
内层未去重	找到答案后 l++、r-- 并继续跳过重复值	避免同一组数字多次入队
双指针边界条件	while (l < r) 且移动后仍需 l < r 再比较	防止越界

42《接雨水》

思路

参考：https://www.bilibili.com/video/BV1CmtZePErE/?spm_id_from=333.337.search-card.all.click&vd_source=3d6f8c0411732bf46c8dda7d2d09a422

• 双指针 + 单调极值：
  • 用 left、right 从两端向中间逼近。
  • 用 maxL、maxR 分别记录已扫描部分的左右最高挡板。
• 每次移动短板：
  • 若 height[left] < height[right]，说明左侧“桶壁”更低，由 maxL 决定当前能接多少水；反之右侧由 maxR 决定。
• 计算并累加：
  • 当前列能接的水 = maxL - height[left]（或 maxR - height[right]），若为负则视为 0（由于 maxL 始终 ≥ height[left]，实际不会出现负值）。
• 时间 O(n)，空间 O(1)。

代码

class Solution {
    public int trap(int[] height) {
        int res = 0;
        int left = 0, right = height.length - 1;
        int maxL = 0, maxR = 0;

        while (left < right) {
            if (height[left] < height[right]) {
                maxL = Math.max(maxL, height[left]); // 更新左侧最高挡板
                res += maxL - height[left];          // 左侧当前列可接水量
                left++;                              // 移动短板
            } else {
                maxR = Math.max(maxR, height[right]);// 更新右侧最高挡板
                res += maxR - height[right];         // 右侧当前列可接水量
                right--;                             // 移动短板
            }
        }
        return res;
    }
}

复杂度

时间：O(n)，每个位置最多访问一次。
空间：O(1)，仅用常数级指针。

易错点

易错点	正确做法	备注
移动高板	必须移动 短板	移高板不会增加水量
maxL/maxR 未实时更新	每次进入分支前 Math.max	保证挡板是当前最大
结果可能为负	由于 maxL ≥ height[left] 等，不会出现负值	无需额外判断
边界循环条件	while (left < right)，不能取等号	两指针相遇时已完成计算

滑动窗口

3《无重复字符的最长子串》

思路

• 滑动窗口（双指针 + 哈希表）
  • left：窗口左边界（闭）
  • i：窗口右边界（开，即当前字符下标）
• 哈希表 map 保存 每个字符最近出现的位置。
• 核心逻辑：
  1. 若当前字符 s.charAt(i) 已存在于窗口内，把 left 跳到 该字符上次出现位置的下一个位置（取 max 防止回退）。
  2. 更新 map 及当前字符位置。
  3. 计算窗口长度并更新全局最大值。

代码

class Solution {
    public int lengthOfLongestSubstring(String s) {
        int left = 0;
        int maxLen = 0;
        Map<Character, Integer> map = new HashMap<>();

        for (int i = 0; i < s.length(); i++) {
            char c = s.charAt(i);
            // 若字符已出现过且位于当前窗口内，则移动左边界
            if (map.containsKey(c)) {
                left = Math.max(left, map.get(c) + 1);
            }
            // 更新字符最近位置
            map.put(c, i);
            // 更新最大长度
            maxLen = Math.max(maxLen, i - left + 1);
        }
        return maxLen;
    }
}

复杂度

时间：O(n)，每个字符最多被左右指针各访问一次。
空间：O(min(n, |Σ|))，|Σ| 为字符集大小。

易错点

易错点	正确做法	备注
直接 left = map.get(c) + 1 导致回退	用 Math.max(left, map.get(c)+1)	保证 left 只向右移动
忘记更新字符最近位置	map.put(c, i) 必须写在每次循环最后	否则后续无法正确判断重复位置
初始 maxLen 设为 0	空串返回 0，非空至少为 1	代码自洽
用数组代替哈希表	若字符集固定且小（如 ASCII）可用 int[128]	常数级更快

438《找到字符串中所有字母异位词》

思路

• 滑动窗口 + 定长比较：
  • 窗口长度固定为 p.length()。
  • 用两个长度 26 的计数数组 sCount、pCount 分别统计窗口内字符与目标字符频次。
• 三步骤：
  1. 初始化：先把前 pLen 个字符塞进数组。
  2. 首窗口若匹配则记录起点 0。
  3. 窗口每次右移一格：
     • 右端新字符入窗（+1）；
     • 左端旧字符出窗（-1）；
     • 比较两数组，若一致则记录起点 i-pLen+1。

代码

class Solution {
    public List<Integer> findAnagrams(String s, String p) {
        List<Integer> res = new ArrayList<>();
        int sLen = s.length();
        int pLen = p.length();
        if (sLen < pLen) return res;

        int[] sCount = new int[26];
        int[] pCount = new int[26];

        /* 1. 初始化窗口 & p 的计数 */
        for (int i = 0; i < pLen; i++) {
            sCount[s.charAt(i) - 'a']++;
            pCount[p.charAt(i) - 'a']++;
        }
        if (Arrays.equals(sCount, pCount)) res.add(0);

        /* 2. 滑动窗口 */
        for (int i = pLen; i < sLen; i++) {
            sCount[s.charAt(i) - 'a']++;          // 右端新字符入窗
            sCount[s.charAt(i - pLen) - 'a']--;   // 左端旧字符出窗
            if (Arrays.equals(sCount, pCount))    // 完全匹配
                res.add(i - pLen + 1);
        }
        return res;
    }
}

复杂度

时间：O(n)（n 为 s 长度，每次 Arrays.equals 是 O(26) 可视为常数）。
空间：O(1)（两个固定 26 长度数组）。

易错点

易错点	正确做法	备注
窗口左右端更新顺序反了	先 ++ 新字符，再 -- 旧字符	否则计数出错
结果下标忘记 +1	res.add(i - pLen + 1)	记录的是窗口左边界
未处理边界首窗口	初始化后先比较一次	0 位置也可能是答案
使用 List<int[]> 比较	用 Arrays.equals 简洁	长度 26 的数组常数级比较

子串

303《区域和检索 - 数组不可变》

思路

• 前缀和数组：
  • 预处理阶段把原数组转成前缀和 s[]，s[i] = nums[0] + … + nums[i-1]。
  • 查询区间 [left, right] 时只需一次减法：s[right+1] - s[left]，O(1)。

代码

class NumArray {
    private final int[] s;   // 前缀和数组，s[i] = sum(nums[0..i-1])

    public NumArray(int[] nums) {
        int n = nums.length;
        s = new int[n + 1];          // 下标 0 留空/哨兵，方便计算
        for (int i = 0; i < n; i++) {
            s[i + 1] = s[i] + nums[i];
        }
    }

    // 查询区间 [left, right] 的和
    public int sumRange(int left, int right) {
        return s[right + 1] - s[left];
    }
}

/**
 * Your NumArray object will be instantiated and called as such:
 * NumArray obj = new NumArray(nums);
 * int param_1 = obj.sumRange(left, right);
 */

复杂度

• 构建：O(n)
• 查询：O(1)
• 空间：O(n)，额外一个前缀和数组。

易错点

易错点	正确做法	备注
前缀和数组长度设错	new int[n + 1]	便于统一 s[i+1] = s[i] + nums[i]
查询区间边界写错	s[right + 1] - s[left]	left、right 都是闭区间
负数或空数组未处理	题目保证非空 & 下标合法	无需额外判断
每次查询仍用循环累加	用前缀和一次减法	否则退化成 O(n) 查询

560《和为 K 的子数组》

思路

• 前缀和 + 哈希表：
  • 维护一个前缀和到出现次数的哈希表。
  • 把「求子数组和等于 k」转化为「找前缀和之差等于 k」。
  • 公式：count += pre.getOrDefault(sum - k, 0)，即已出现过的前缀和中有多少个满足 sum[i] = sum - k。
• 初始化：空前缀和 0 出现 1 次，用于处理「从首元素开始」的子数组。

当然也可以两层循环：

class Solution {
    public int subarraySum(int[] nums, int k) {
        int n = nums.length;
        int count=0;
        int[] preSum = new int[n+1];
        preSum[0]=0;
        for(int i=0;i<n;i++){
            preSum[i+1]=preSum[i]+nums[i];
        }

        for(int i=0;i<n;i++){
            for(int j=i;j<n;j++){
                if(preSum[j+1]-preSum[i]==k){  // 如果写成 preSum[j] - preSum[i]，那就是 nums[0..j-1] - nums[0..i-1]，少算了 nums[j]。因此必须用 j+1 来包含到下标 j 的元素。
                    count++;
                }
            }
        }
        return count;
    }
}

代码

class Solution {
    public int subarraySum(int[] nums, int k) {
        Map<Integer, Integer> pre = new HashMap<>();
        pre.put(0, 1);                         // 空前缀和出现 1 次
        int sum = 0, count = 0;

        for (int num : nums) {
            sum += num;                                   // 当前前缀和
            count += pre.getOrDefault(sum - k, 0);        // 统计差值为 k 的个数
            pre.put(sum, pre.getOrDefault(sum, 0) + 1);   // 记录当前前缀和
        }
        return count;
    }
}

复杂度

• 时间：O(n) —— 单次遍历。
• 空间：O(n) —— 哈希表最坏存 n 个不同前缀和。

易错点

易错点	正确做法	备注
未初始化 pre.put(0, 1)	空区间前缀和为 0 出现 1 次	否则漏掉从首元素开始的子数组
先累加 count 再更新 pre	顺序正确即可	先查旧值，再存新值
使用数组而非哈希表	若数据范围小可用数组，但哈希表更通用	范围大时哈希表更省空间
忘记处理负数或 0	无需特殊处理，前缀和算法天然支持	负数、0、正数均可

239《滑动窗口最大值》

思路

• 单调双端队列：
  • 队列 deque 保存窗口内可能成为最大值的下标，且对应值单调递减。
• 滑动窗口五连击（每步都在 O(1)）：
  1. 移除过期：队首下标若已滑出窗口左边界，则出队。
  2. 维护单调：从队尾弹出所有小于当前值的元素。
  3. 入队：把当前下标加入队尾。
  4. 记录答案：当窗口长度达到 k 时，队首即为当前窗口最大值，写结果。

代码

class Solution {
    public int[] maxSlidingWindow(int[] nums, int k) {
        if (nums == null || nums.length == 0) return new int[0];

        Deque<Integer> deque = new LinkedList<>();
        int n = nums.length;
        int[] res = new int[n - k + 1];

        for (int i = 0; i < n; i++) {
            // 1. 移除已滑出窗口的过期下标
            if (!deque.isEmpty() && deque.peek() < i - k + 1) {
                deque.pollFirst();
            }

            // 2. 保持单调递减：队尾比当前值小的全部弹出
            while (!deque.isEmpty() && nums[deque.peekLast()] < nums[i]) {
                deque.pollLast();
            }

            // 3. 当前下标入队
            deque.offerLast(i);

            // 4. 窗口形成后，队首即为最大值
            if (i >= k - 1) {
                res[i - k + 1] = nums[deque.peekFirst()];
            }
        }
        return res;
    }
}

复杂度

• 时间：O(n)，每个元素最多入队、出队一次。
• 空间：O(k)，队列最多存储 k 个下标。

易错点

易错点	正确做法	备注
队列只存值不存下标	必须存下标，才能判断窗口边界	否则无法定位过期元素
未检查队首是否过期	每次循环先 peek() < i-k+1 再移除	避免旧值干扰
维护单调时误用 pollFirst()	应从队尾弹出	保持单调递减
结果数组长度写错	n-k+1	窗口数量为 n-k+1
队首取值用 poll()	用 peekFirst() 只读不移除	避免破坏队列结构

76《最小覆盖子串》

思路

• 滑动窗口 + 固定字符频次
  • 用两个长度 128 的数组 sCount、tCount 分别统计窗口内和目标串 t 的字符出现次数。
  • isCovered 判断当前窗口是否已满足 每种字符频次 ≥ t 的需求。
• 滑动窗口三步骤：
  1. 右指针扩张窗口，把字符加入 sCount。
  2. 当窗口满足条件时，尝试左指针收缩，更新最短子串。
  3. 左指针移动时，把移出的字符频次减回，并重新检查是否仍满足条件。
• 若遍历完仍无满足条件的窗口，返回空串。

代码

class Solution {
    public String minWindow(String s, String t) {
        int[] sCount = new int[128];
        int[] tCount = new int[128];
        int m = s.length(), n = t.length();
        if (m < n) return "";

        /* 1. 统计 t 的字符需求 */
        for (char c : t.toCharArray()) tCount[c]++;

        int left = 0;
        int ansLeft = -1, ansRight = m;

        /* 2. 滑动窗口 */
        for (int right = 0; right < m; right++) {
            sCount[s.charAt(right)]++;          // 右端字符入窗

            while (isCovered(sCount, tCount)) { // 窗口满足条件
                if (right - left < ansRight - ansLeft) {
                    ansLeft = left;
                    ansRight = right;
                }
                sCount[s.charAt(left)]--;       // 左端字符出窗
                left++;
            }
        }

        /* 3. 返回结果 */
        return ansLeft == -1 ? "" : s.substring(ansLeft, ansRight + 1);
    }

    /* 判断窗口是否满足 t 的字符需求 */
    private boolean isCovered(int[] cntS, int[] cntT) {
        for (int i = 0; i < 128; i++) {
            if (cntS[i] < cntT[i]) return false;
        }
        return true;
    }
}

复杂度

• 时间：O(|s| + |t|)
  每个字符最多入窗、出窗各一次；isCovered 遍历固定 128 次视为常数。
• 空间：O(1)
  仅用两个长度 128 的计数数组。

易错点

易错点	正确做法	备注
未初始化 ansLeft = -1	用于判断是否有解	无解返回空串
未处理大小写或字符集	cnt[128] 覆盖 ASCII	也可改成 256
isCovered 遍历范围写错	从 0 到 127 统一判断	避免漏掉符号或数字
返回子串时越界	ansLeft == -1 ? "" : s.substring(...)	防止 substring(-1, ...)